Linje som går igenom cirkel, koordinater

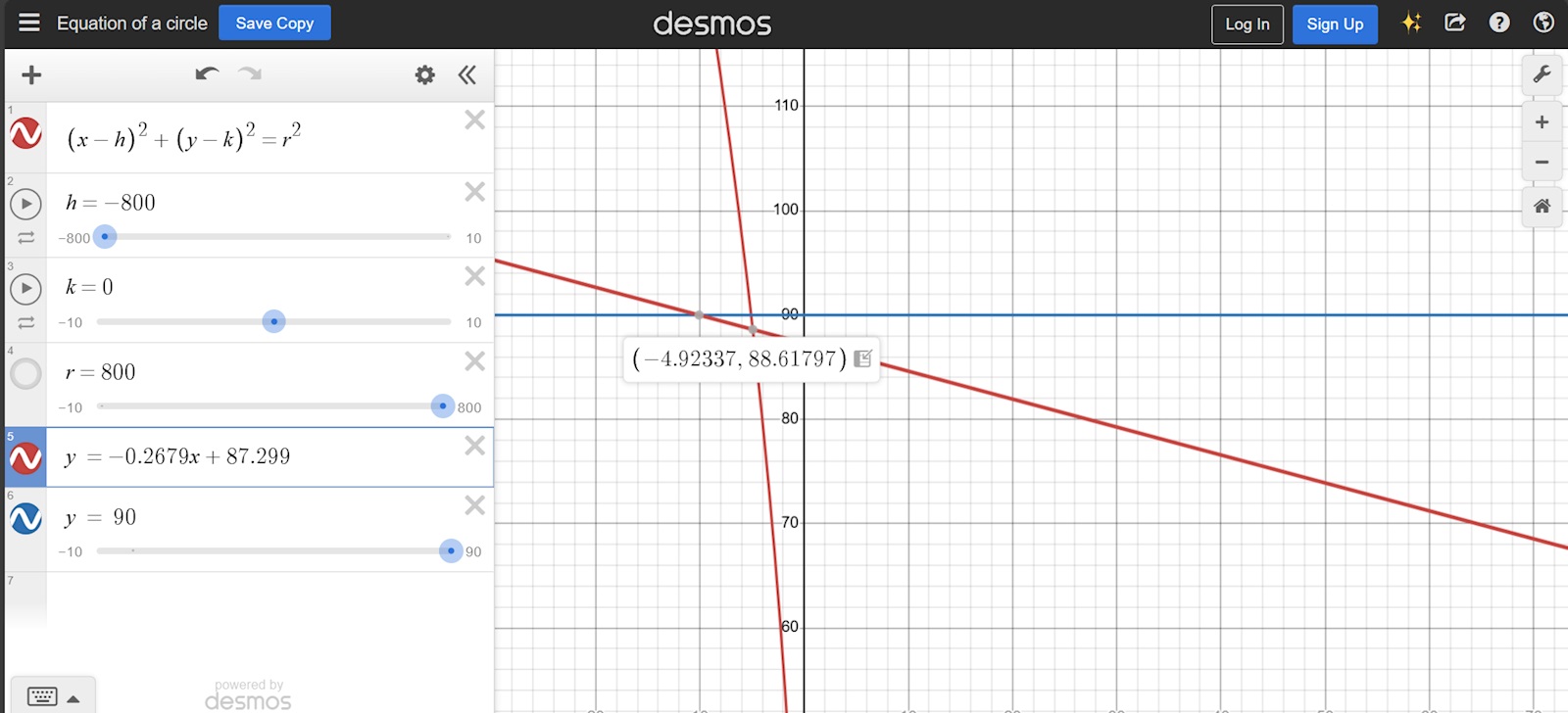
”Cirkeln har R= 800 och centrum ligger på -800 i x och y i origo.”

Jag tror du menar att cirkelns centrum är (–800, 0). Origo har inte med centrum att göra.

I så fall är cirkelns ekvation

(x+800)² + y² = 800²

[OBS det är plus; (x–(–800))² = (x+800)². ]

Sedan ska du inte skriva X och Y när du menar x och y. Och hellre x tan15 än tan(15)x.

Du får alltså

(x+800)² + (–xtan15° + 87,299)² = 800²

Jag håller med om att det ser räligt ut, men i grund och botten är det en vanlig andragradare. Med flit och omsorg bör den kunna knäckas.

Marilyns ekvation är antagligen snabbare, men du kan också lösa uppgiften med enkla trigonometriska samband, eftersom en 15^o-vinkel är given. Ett antal steg, men små steg. Jag fick x $\approx$ -4,923.

Okej, tack 🙂

Men jag ser inte vad du menar riktigt. Hittar ej den väsentliga informationen. Hittar massa vinklar men aldrig allt jag behöver.

Löste ekvationen.

Är du intresserad av att se en trigonometrisk lösning (utan cirkelns ekvation)?
Eller tycker du att det räcker med din lösning?

Jag är intresserad av alla tänkbara lösningar på problemet.

Jag ser följande utifrån det du ritat upp

Nej, jag ser. "Tangenttriangeln" som konstrueras där har vinkeln 15° ovanför x där, vilket medför att man kan göra en rätvinklig triangel med kateten 800 och vinkel 15° pga likformighet. Sedan kan man räkna ut hypotenusan på den och ta det avståndet-800 så har man hypotenusan på den översta lilla triangeln där.

Så kan man sedan lösa kateten x

Eller, nej, förresten, det går inte heller:p

Först översiktligt. Sedan kan jag visa mer detaljerat om det behövs.

1. OB = 87,299/tan 15^o.

2. AB = AO + OB.

3. Vi kan nu beräkna vinkel ADB med sinussatsen.

4. Därefter vinkel OAD (triangelns vinkelsumma).

5. Halvera den så har du vinkel OAC (triangeln OAD likbent, höjden AC delar OAD mitt itu).

6. Den vinkeln är lika med vinkel DOE.

7. OC = 800 sin(vinkel OAC). OD = 2*OC

8. x = OD * sin(vinkel DOE).

Hoppas jag skrivit rätt.

Oj var det så invecklat! Det hade jag aldrig tänkt på kan jag ju säga. Ganska kul lösning med massa olika metoder/regler.

Jag fattar iaf, tack.

Kanske finns andra sätt. Det tyngsta inslaget var sinussatsen. De andra stegen var små.

Att jag själv tycker att geometriska problem är roliga är för hur man får fundera hur man ska ta sig fram genom figuren. Vilka vägar man kan ta (i vilken ordning man beräknar vinklar och sträckor) och med vilka regler. Tills man når målet. Lite som i ett äventyrsspel.

Förstår. 

Jag tycker det är lite för svårt för att jag ska tycka det är kul, blir mest jobbigt/frustrerande.

Ok. Det ör ganska avancerade uppgifter du kommer med.

Louis skrev:

Ok. Det ör ganska avancerade uppgifter du kommer med.

Jag tycker det är intressant/kul. Men är inte tillräckligt duktig för att kunna använda mig av alla metoder på ett effektivt sätt, kanske behöver fundera över vad sinussatsen egentligen var för någonting till att börja med. Sen då att identifiera att jag kan använda mig utav dem, det är lite.. ja, väsentligt. Så, om jag var mycket mer med på vad jag håller på med skulle det kännas bättre.

Men! Det här är ett irl problem, och är inte riktigt van med att problemen kan behöva sådär många steg så övervägde egentligen inte ens den möjligheten. Kanske en skillnad i perspektiv kan göra en del.

Min favorit hittills var ett annat problem som vi tittade på för något år sedan eller så när man behövde ta reda på skärningspunkter på en cirkel utifrån ganska lite information. Du hade lika då någon geometrisk lösning mer, medans jag hade två stycken ekvationer för två linjer.. osv. Det tyckte jag var kul. Sen hjälpte du mig att algebraiskt lösa någon ekvation för en triangel som otroligt enkelt hade kunnat blivit löst med cosinussatsen, var helt otroligt frustrerad över det. Tog otroligt lång tid! :P Nu hade jag kunnat använda mig av båda metoderna där väldigt enkelt, så, det är ju kul.

Trigonometri är egentligen ett område där jag glömt det mesta.Jag fick kolla upp vad sinussatsen säger.

Här hade vi en triangel där vi visste två sidor och en vinkel och ville beräkna en vinkel till.
Då inventerar man verktygslådan och finner att sinussatsen var just vad vi behövde.

Sedan löste du uppgiften på ett helt annat sätt.

Ja. Ska försöka ändra perspektiv lite. 

Egentligen ska det vara en liten cirkel R3 tangent till både linjen 15° och R800 på insidan vid vinkel D och vinkeln ovanför D där, precis i hörnet vid skärningspunkten. Det kunde lösas ändå så hoppade över det här, och för att det kändes väldigt komplicerat.

Men Jag tror att punkt D skulle vara en tangent till den cirkeln (eller snarare vinkeln därifrån), så har man den vinkeln D där och faktumet att det är 90° till cirkelns centrum borde man bara kunna rita upp en liten triangel där och navigera sig ifrån X koordinaten till skärningspunkten. Eller så är det mer komplicerat.

Typ såhär.

Menar du så här?

Jag kan inte följa dina tankar. En punkt kan inte vara tangent till något, inte heller en vinkel.

Jag ser inte sambandet mellan den lilla cirkeln och problemet att finna x.
Vet man något mer om den lilla cirkeln?

Varifrån kommer uppgiften?

Har du en bild du kan ladda upp?

Jag har inte verktygen till att rita upp det på ett bra sätt. 

Gjorde följande för hand nu.

Det jag skrivit ut är informationen att tillgå. Cirkeln R3 är tangent till linjen 15° och radien 800. Man vill hitta koordinaterna för dessa punkter i y och x. Vet inte hur man ska tänka med R800 där

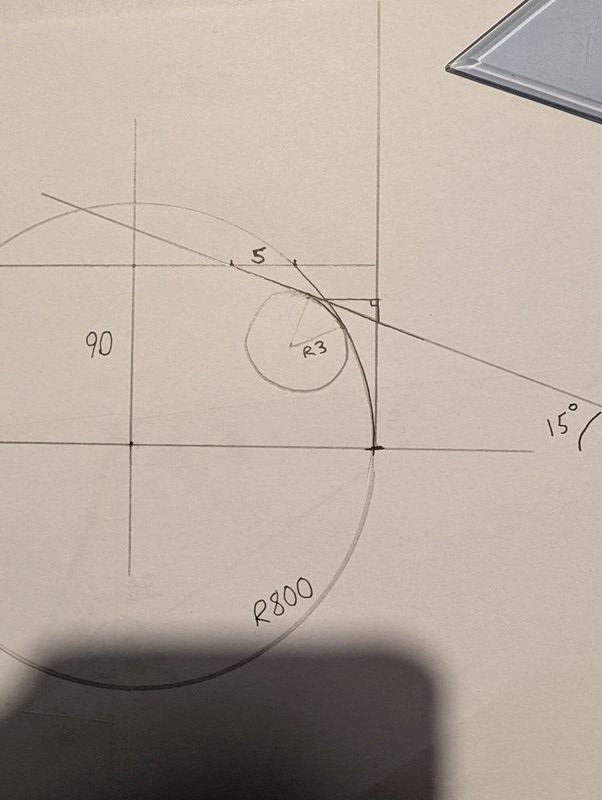
Yngve skrev:

Varifrån kommer uppgiften?

Har du en bild du kan ladda upp?

Det är ifrån en cad ritning. Kan inte lägga upp någon bild tyvärr.

Är det koordinaterna för den lilla cirkelns tangeringspunkter som ska beräknas?

Ett helt nytt problem alltså?

Vad står 90 och 5 för?

Ja, precis.

Ja, eller, jag trodde föregående var ett steg på vägen för det här problemet.

90 är måttet ifrån centrum på R800 till linjen som går parallellt med x axeln. Mått 5 är, om vi låter R800 gå mot mått 90, sträckan ifrån där de möts och till punkten där 15° linjen skär igenom den linjen.

Den får vi ju enkelt med pythagoras sats bara. 800-sqrt(800^2-90^2) = 5.0786.

Alltså är totala sträckan 5.0786+5 = 10.0786 ifrån X0.

Slängde ihop det här lite snabbt, är inte så duktig på det men borde vara lite tydligare:

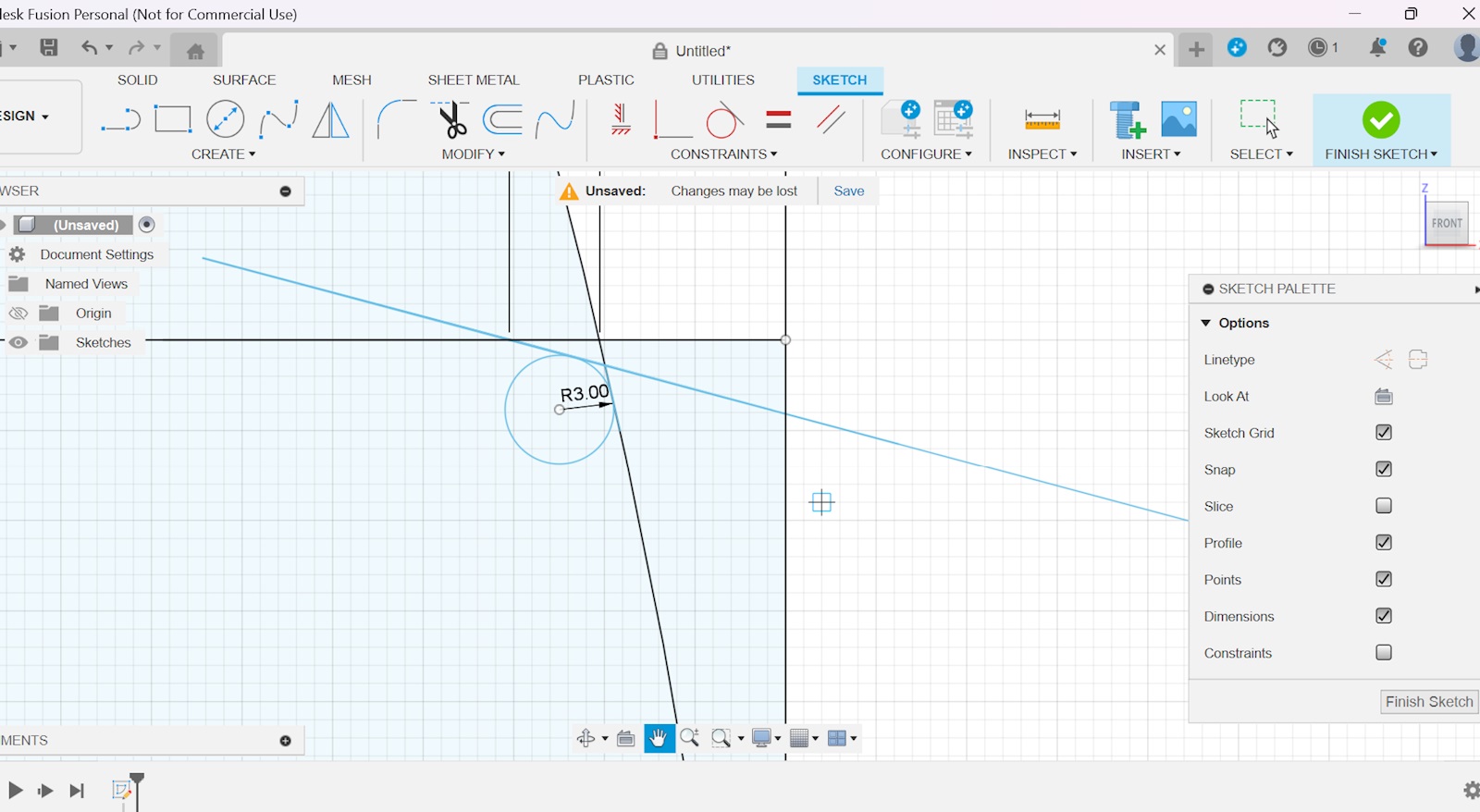
Men då är väl inte sträckan  5,0786 där du skrev 5? Utan sträckan höger om.
Har måttet 90 någon betydelse för lösningen på uppgiften?

Ja precis, det stämmer. Nej det är måttet ifrån x0y0 som är intressant (som alltså är vinkel0° på R800). Fast, resultatet i sig är inte så intressant utan mer hur man kommer fram till det.

Vad är x0y0? Stora cirkelns medelpunkt?
Måttet till vad?
Vad menar du med "vinkel0° på R800"?

Jag tror mig se en trigonometrisk lösning i rätt många steg.

Nej, om man tänker sig att stora cirkeln är enhetscirkeln så är X0,y0 vid Sin(0), dvs (1,0). Centrum är -800 till centrum på diameter 1600 cirkeln

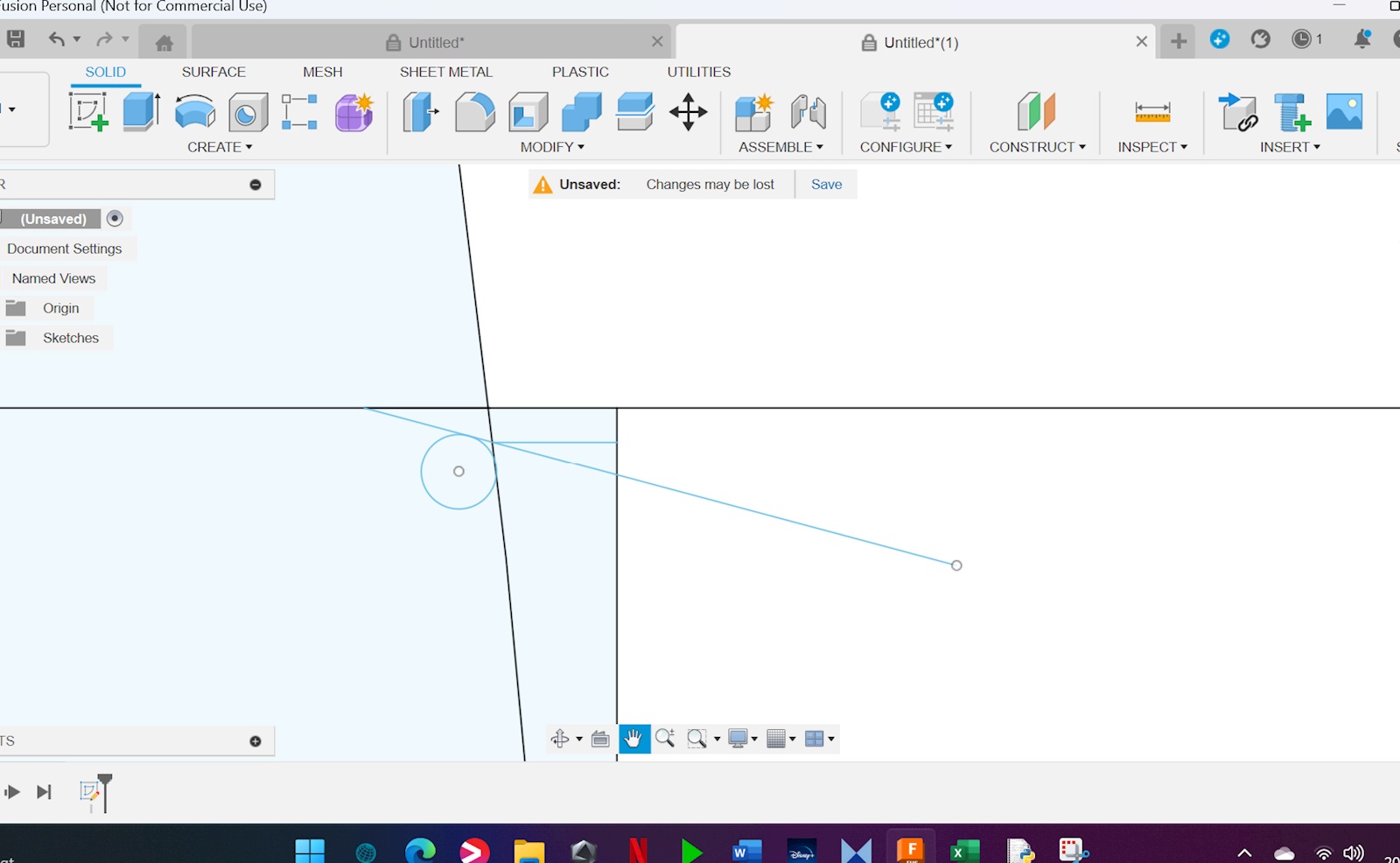
x0,y0, aka origo (0, 0).

det är måttet ifrån x0y0 som är intressant

Måttet till vad?

TangeringsPunkterna på lilla cirkeln

Är det inte koordinaterna för tangeringspunkterna som du vill ha? Som du skrev förut.
Med koordinaterna kan du förstås beräkna avstånden, men vilket är slutmålet för uppgiften?

Förstår inte riktigt. Cirkel R3 är tangent till R800 och linjen 15°, detta bildar två stycken punkter på respektive tangeringspunkt. Det som är intressant är avståndet ifrån origo till dessa två olika punkter för y,x respektive. Intressant är väl också vart på cirkel R3 R800 tangerar och vilken vinkel en tangent linje skulle ha där.

två stycken punkter på respektive tangeringspunkt

Menar du x- och y-koordinat?

Intressant är väl också var på cirkel R3 R800 tangerar

Är inte det den ena tangeringspunkten av dem som du skriver om i meningen innan?

och vilken vinkel en tangent linje skulle ha där

En ny uppgift? Men den vinkeln får man nästan på köpet.

Man kanske kan göra på andra sätt, men så här tänker jag mig en trigonometrisk beräkningsordning:

1. Cosinus
2. Minus
3. Tangens
4. Sinussatsen
5. Triangelns vinkelsumma
6. Sinus, cosinus på triangeln med hypotenusa 800

För tangeringspunkten med linjen:
Beräkna koordinaterna för lilla cirkelns medelpunkt (sinus, cosinus på triangel med hypotenusa 797).
Därefter sinus, cosinus på hypotenusan 3.