Linjärtkoordinat byte

Hej, Jag försöker att lösa denna uppgift. Rätt svar ska vara 16.

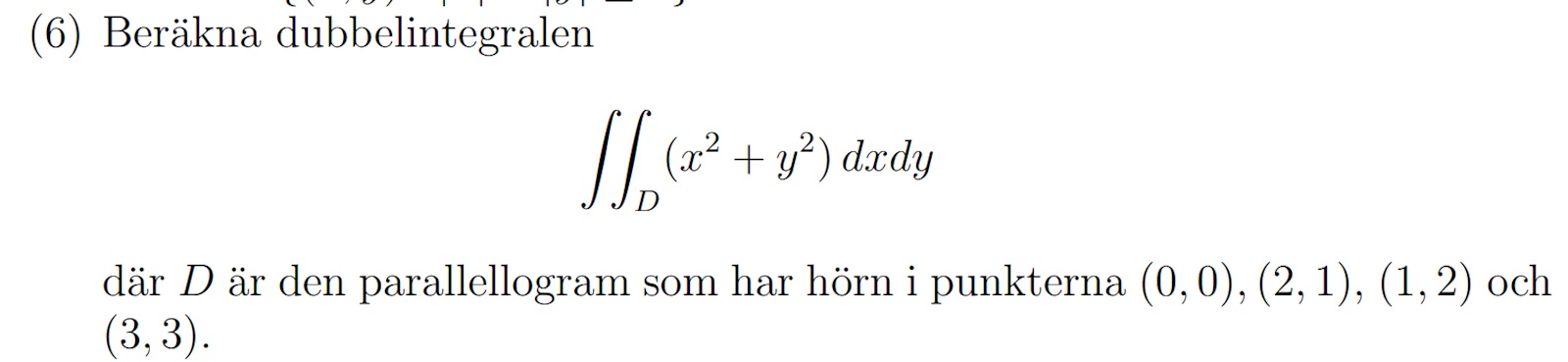
Jag börjar med att rita upp figuren (parallellogrammet) och konstaterar att den lnte har sitt centrum i origo. Jag konstaterar att jag behöver flytta figuren 1,5 steg åt vänster i x-led och och 1,5 steg ner i y-led. Stämmer verkligen detta? Känns konstigt att ha 1,5 x och y.

Hur som hellst det ger mig avbildningen (x,y) --> ((x-1,5),y-1,5))

Jag sätter:

u = u0 + x +y

v=v0 + x -y

Jag räknar ut u0=0 och v0=-3

Har jag gjort rätt till hit?

Jag blir osäker på hur jag ska räkna ut funktionsdeterminaten eftersom att jag har 2 rader och 3 kolumner.

Vilka kommer mina gränser bli i mitt nya område (E)?

Länk till lämplig sida uppskattas

lösningförslag bild:

Man skulle kunna sätta (x, y) = u(2, 1) + v(1, 2), med 0 <= u, v <= 1.

PATENTERAMERA skrev:
Man skulle kunna sätta (x, y) = u(2, 1) + v(1, 2), med 0 <= u, v <= 1.

Kan du utveckla? Förstår ej

Du kan ju se parallellogrammen som ”uppspänd” av vektorerna (2, 1) och (1, 2) så att varje punkt (x, y) i parallellogrammen kan skrivas som en linjärkombination u(2, 1) + v(1, 2) av dessa vektorer (där du får välja u, v fritt mellan 0 och 1).

Så du kan transformera integralen till en integral över en kvadrat med sidan 1 i uv-planet.

x = 2u + v

y = u + 2v.

Integranden blir kanske inte jätteenkel men området är ju trevligt.

PATENTERAMERA skrev:
Du kan ju se parallellogrammen som ”uppspänd” av vektorerna (2, 1) och (1, 2) så att varje punkt (x, y) i parallellogrammen kan skrivas som en linjärkombination u(2, 1) + v(1, 2) av dessa vektorer (där du får välja u, v fritt mellan 0 och 1).

Så du kan transformera integralen till en integral över en kvadrat med sidan 1 i uv-planet.

x = 2u + v

y = u + 2v.

Integranden blir kanske inte jätteenkel men området är ju trevligt.

tack för hjälpen! nu fårstår jag bättre. Jag täknte för hur jag kunde uttrycka den första vektorn som en funktion: y=x/2 vilket omskrivning ger 2y-x som jag kallar för u. Gör samma sak med andra och får v=2x-y och därefter kunde jag lösa som vanligt.

Jag testa att tänka igenom resonemangen för att kalla x=2u+v och y=1u+2v. Då blir det min nya bas och jag tänker mig att jag ska gå från punkten (0,0) till (1,1). Som de ger min att jag kommer att integrera från 0 till 1 istället för 0 till 3, och funktionsdeterminaten blir 3 istället för 1/3. Tror att det totalt sätt kommer att smidigare lösningar med det basbyte som du föreslog.

Lösningsförslag:

Jag har lite svårt att följa med i vad du gör.

Så här tänker jag.

Avbildningen (u, v) $\mapsto$ (x(u, v), y(u, v)) = (2u + v, u + 2v) avbildar kvadraten K = [0, 1] $\times$ [0, 1] i uv-planet på vår parallellogram D i xy-planet.

$\frac{\partial (x, y)}{\partial (u, v)}$ = 3.

$I = \iint_{D} (x^{2} + y^{2}) d x d y = \iint_{K} ({(2 u + v)}^{2} + {(u + 2 v)}^{2}) \frac{\partial (x, y)}{\partial (u, v)} d u d v = \int_{0}^{1} \int_{0}^{1} (5 u^{2} + 5 v^{2} + 8 u v) 3 d u d v$ .

$\int_{0}^{1} \int_{0}^{1} u^{2} d u d v = \int_{0}^{1} d v \cdot \int_{0}^{1} u^{2} d u = 1 / 3 .$

$\int_{0}^{1} \int_{0}^{1} u v d u d v = \int_{0}^{1} u d u \cdot \int_{0}^{1} v d v = 1 / 4$ .

I = 3(5/3 + 5/3 + 8/4) = 16.

Svara

Visa senaste svar