Linjär Optimering, Blanda saft.

Villes Supersaft är en blandning av två saftsorter. Saft A har en koncentration på 15% och kostar 40 kr per liter medan saft B har en koncentration på 25% och kostar 55 kr per liter. Ville har listat ut att smaken blir bäst om blandningens koncentration är minst 17% och maximalt 18%. Till en fest behövs minst 30 liter Supersaft. Det visar sig att han har kvar 7 liter av saft B sedan tidigare som han kan använda om han vill. Hur många liter av saft A måste han köpa för att få så billig Supersaft som möjligt?

Jag förstår att ett ekvations system ska ställas upp och att säg om Saft A är x och Saft B är y, är

x>0

y>0

x*? + y*? = 30liter

men här tar det stopp.

Du skriver att "Saft A är x" och "Saft B ör y". Menar du då att du tar x liter av Saft A och y liter av Saft B?

I så fall är dina villkor

$x\geq0$ (Kan inte använda en negativ volym av Saft A)
$y\geq0$ (Kan inte använda en negativ volym av Saft B)
$y\leq7$ (Kan använda maximakt 7 liter av Saft B)
$x+y\geq30$ (Det ska bli minst 30 liter saft)
$0,17\leq\frac{0,15x+0,25y}{x+y}\leq0,19$ (Saften ska bli god)

Kostnaden, som ska minimeras, är $K=40x+55y$

Hej, Tack!

När jag försöker lösa ekationssystemet med geogrebra får jag ett område där svaret bör vara inom, som man ser på bilden. Men området fortsätter så som bilden visar längs hela x-axeln,hur ska jag då veta vad som är antal liter saft A? Eller är det där den korsar x-axeln då den har lägst värde?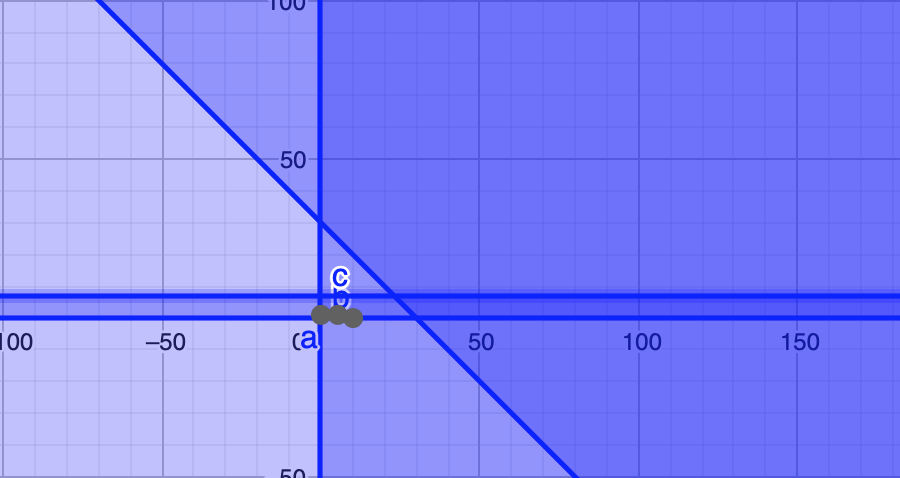

Kan du förklara vad områdena du har ritat betyder?

Det är ekvationssystemet som du hjälpte mig med

Jag ser bara 4 villkor visualiserade i koordinatsystemet. Men jag skrev 5 villkor.

Vänta ojdå!, jag fattar inte hur man lägger in sista villkoret i geogebra.

Vi vet att x+y är ett positivt tal, vilket gör att vi kan multiplicera hela den olikheten med x+y och därmed få en enklare olikhet att visualisera i koordinatsystemet.

jaha! okej fattar nu, tack för hjälpen!

Svara

Visa senaste svar