Linjär optimering

Henrik 2 skrev:

Hej,

Behöver inte ta själva frågan utan har kommit fram till (linjär optimering) följande villkor/ olikheter:

y$\ge$2x (dvs man ska baka minst dubbelt så många y som x, stämmer det att ställa upp villkoret/olikheten så?)

50x+80y=35 000 (tillverkningskostnad  50 kakor och 80 bakelser)

x$\ge$0

y$\ge$0

Vinstfunktion 30x+40y

Hur beräknar man denna algebraisk så olikheterna (likheterna) skär varandra o få fram de relevanta områdena, hörnpunkterna, dvs koordinaterna (x,y)?

Förstår o kan räkna ut 50x+80y=35 000  för att få fram x o y koordinater

Men hur blir y=2x med dess hörnkoordinater av x o y. Om y=2x vad blir x för att få fram koordinater av den linje/villkoret?

Och hur får man att dem skär varandra dessa två om/när man räknar ut det algebraiskt för att kombinera maxmimal vinst?

Mvh/H

Det är svårt för oss att veta hur man har kommit fram till de olika olikheterna om vi inte har själva uppgiften.

Om det inte är det du vill ha hjälp med utan nästa steg, så gäller det att rita upp de olika olikheterna. Jag brukar föredra att rita upp de ekvationer som är gränserna för olikheterna och sedan fundera på vilken sida om linjen man vill vara, eftersom olikheter är ett otyg som är lätt att göra fel på.

Nu vet jag itne om detär den högra eller vänstra triangeln som är intressant, men troligen skall det inte vara ett likhetstecken 50x+80y=35 000 (tillverkningskostnad 50 kakor och 80 bakelser) utan 35 000 kr är övre gränsen för vad man har råd med, d v s det är den hägra triangeln som är intressant. Beräkna värdet för målfunktionen 30x+40y för de båda hörnen som inte är origo, där värdet självklart är 0.

Hej,

Jo, hur jag kommit fram till det spelar mindre roll här, utan vill som sagt veta o förstå nästa steg utifrån villkoren. Jag kan rita upp det,visst,e dock osäker på hur man ritar, men jag räknar hellre ut det algebraiskt då det är det som jag lärt mig nu.

Man kan sätta= istället för olikheter har jag fått lära mig som underlättar beräkningen.

Men förstår inte din förklaring riktigt utan behöver få se hur man algebraiskt får fram koordinatera x och y utifrån de villkor som jag ställt upp.

Mvh/H

För att beräkna algebraiskt kan man använda exemplevis simplexmetoden, men det ligger nog på universitetsnivå.

Annars gäller att optimum ligger på kanten eller i hörnen på det område som innesluts av de villkor du har.

När du ritat upp området kan du testa vad vinstfunktionen får för värden i hörnen, (det brukar bara vara några enstaka hörn att testa på, om två närliggande hörn har samma vinstvärde så ligger optimum utefter hela kanten mellan hörnen.

Henrik 2 skrev:

[...]

förstår inte din förklaring riktigt utan behöver få se hur man algebraiskt får fram koordinatera x och y utifrån de villkor som jag ställt upp.

I den här tråden beskrev jag för dig hur du kan göra för att få fram detta algebraiskt.

Henrik 2 skrev:

Hej,

 

Jo, hur jag kommit fram till det spelar mindre roll här, utan vill som sagt veta o förstå nästa steg utifrån villkoren. Jag kan rita upp det,visst,e dock osäker på hur man ritar, men jag räknar hellre ut det algebraiskt då det är det som jag lärt mig nu.

Man kan sätta= istället för olikheter har jag fått lära mig som underlättar beräkningen.

Men förstår inte din förklaring riktigt utan behöver få se hur man algebraiskt får fram koordinatera x och y utifrån de villkor som jag ställt upp.

Mvh/H

Även om du ritar upp området kan man behöva lösa ekvationerna för att hitta värdena på x och y, men det är enklare att se om man har räknat rätt om man har en bild att luta sig mot.

Jag hade tänkt lägga in bilden också, men det missade jag tydligen. Här kommer den:

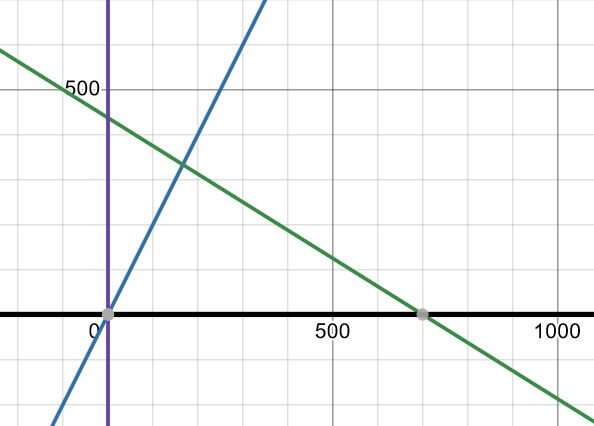
Här kan jag läsa av att om y = 0 så är x = 700 (men det är bäst att kolla så att det stämmer exakt, jag kan inte se skillnad på om x har värdet 690 eller 713) men den andra "korsningen" (mellan grön linje och ljusblå linje) behöver jag räkna ut algebraiskt. Om jag då får fram att x är mellan 150 och 200 och y ligger mellan 300 och 350 så ser det ut att stämma med min bild.

Hej alla,

Tack för input. Men förstår fortfarande inte hur man beräknar vilkoret/olikheten/likheten

y≥ 2x

(dvs man ska baka minst dubbelt så många y som x, stämmer det att ställa upp villkoret/olikheten så här då?)

Y, jag har lärt mig det som du lärt mig algebraiskt men denna har jag inte lärt mig hur man beräknar algebraiskt, d v s y≥ 2x.  Kan du,annan, hjälpa mig med det så jag kommer fram till x o y koordinater för detta villkor?

Och sedan tar jag detta villkor med det andra villkoret och ser/får ut vart de skär varandra . Därefter så tar jag vinsfunktionen o beräknar optimum/maximal vinst.

Ah, eftersom jag inte har sett själva uppgiften har jag tolkat lite fel. Punkten där den gröna linjen skär x-axeln är ointressant, eftersom det skulle vara mer än dubbelt så många y som x, så det är punkterna (0,0) (där vinstfunktionen är 0), (0,fyrahundranånting) och  (ungefär 170, ungefär 330) som är intressanta. För att ta reda på var funktionen 50x+80y = 35 000 skär y-axeln sätter vi in x = 0, så ekvationen blir 80y = 35 000 => y = 437,5, fast halva bakelser funkar inte. För att ta reda på den tredje punkten löser vi ut y ur ekvationen och likställer den med y = 2x, så 437,5-5x/8 = 2x. Denna ekvation har lösningen x = 166,666... så y = 333,333...

Man kan bara baka hela kakor och bakelser, så testa vad vinstfunktionen blir för (166, 333) och för (0,437).

Hej,

Tackar. Ok, så fick nu fram alla koordinater för olikheterna/linjerna då man sätter 437,5-5x/8 = 2x. för linje 3 o då får man ut x o y koordinaterna för denna också.

Efter avrundning fick jag ut koordinaterna (0,0), (0,438) och (167,334)

Sedan beräknas det genom vinstfunktion 30x+40y

Är det alltså bara tre st punkter som kan beräknas i denna med dessa villkor?

Mvh/H

Kom ihåg att linjerna i figuren är begränsningslinjer för respektive olikhet.
Villkoret anger vilken sida om linjen som är förbjuden.

Du får inte vara till vänster om y-axeln
Du får inte vara under x-axeln
Du får inte vara ovanför den gröna linjen
Du får inte vara under den blå

Det som sedan blir kvar är det tillåtna området (inkl resp linje)

Vilka blir här hörnpunkterna i det tillåtna området?

Hej,

Ok, förstår dessa villkor, men jag har lärt mig att beräkna algebraiskt och då är väl dessa koordinater det tillåtna, det som e relevant?

Jaja, men algebraisk bestämning av området är onödigt komplicerat

Följer du denna enkla geometriska metod,
ser du direkt vilka skärningspunkter du måste beräkna.
Dessa är nämligen hörnpunkterna i det tillåtna området
och dem måste du beräkna, men inga andra.

Pröva båda metoderna och se vad du tycker.

Okidoke,tackar,har dock lärt mig att beräkna algebraiskt o e inte lika bra på att se , men ska vara i första kvadranten och kika över/under respektive linje.

Hej,

Se inlägg 9. E det allt som behövs o sedan då räkna ut maxvinst, optimum av vinstfunktionen?

Koordinaterna korrekt, man får inte ut några koordinater o en linje med enbart olik/likheten y≥2x

utan y=2x sätts bara in när man söker skärningspunkter mellan linjerna?

Mvh/H

Henrik 2 skrev:

Hej,

Se inlägg 9. E det allt som behövs o sedan då räkna ut maxvinst, optimum av vinstfunktionen?

Koordinaterna korrekt, man får inte ut några koordinater o en linje med enbart olik/likheten y≥2x

utan y=2x sätts bara in när man söker skärningspunkter mellan linjerna?

Mvh/H

Hej, det är bara nästan rätt.

Du bör alltid kontrollera ditt resultat.

Du har villkoren

• $x\geq0$
• $y\geq0$
• $50x+80y\leq35000$
• $y\geq2x$

Du har kommit fram till de intressanta punkterna 

• (0, 0)
• (0, 438)
• (167, 334)

Har du kontrollerat att dessa punkter uppfyller alla villkor?

• Om ja, vad kom du fram till?
• Om nej, gör det och berätta vad du kom fram till.

Uppgiften är lite lurig eftersom x och y måste vara heltal.

Då är det inte självklart vilka punkter som maximerar målfunktionen.

Om vi tittar närmare på de tillåtna punkterna nära det intressanta hörnet (där y = 2x skär 50x+80y = 35 000) så ser vi följande:

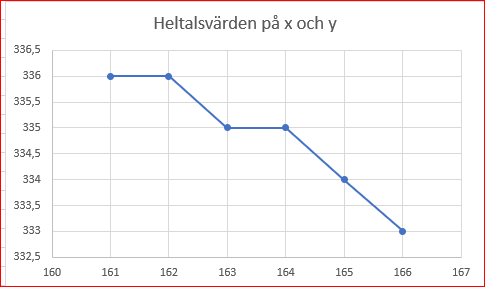
Intressant här är att målfunktionen inte maximeras vid (166, 333) som man skulle kunna tro, utan istället vid (164, 335).

På Matte 3-nivå får man nog använda digitala hjälpmedel för att lösa uppgiften. I det här fallet använde jag Excel. 

Hej Y,

Tror dock inte man behöver vara så noga,e nog bara principen, även om det e bra att förstå att heltal är det som ska vara. Men förklara varför får man inte maxvinst vid avrundning av icke heltal på x o y?

Vet ej hur man kontrollerar att dessa e relevanta, då jag enbart räknar ut dem algebraiskt.

Mvh/H

Henrik 2 skrev:

Hej Y,

Tror dock inte man behöver vara så noga,e nog bara principen, även om det e bra att förstå att heltal är det som ska vara. Men förklara varför får man inte maxvinst vid avrundning av icke heltal på x o y?

Eftersom du måste avrunda neråt för att hålla dig inom tillåtet intervall (se nedan). Att avrunda y-vördet neråt ger stor effekt på målunktionens värde eftersom y där multipliceras med 40 (och x bara med 30).

Vet ej hur man kontrollerar att dessa e relevanta, då jag enbart räknar ut dem algebraiskt.

 

För att en punkt ska vara relevant så måste den ligga i det tillåtna området, vilket betyder att dess koordinater måste uppfylla alla villkor.

Se svar #15.

Jo, jag förstår det Y, me dålig på att se det tilllåtna området,bara tar det,som sagt,algebraiskt.

Ok, så kan man avrunda neråt då när man inte får x o y till heltal?

Mvh/H

Henrik 2 skrev:

Jo, jag förstår det Y, me dålig på att se det tilllåtna området,bara tar det,som sagt,algebraiskt.

Du behöver inte se det tillåtna området, du kan rent algebraiskt kontrollera om en given punkt tillhör området eller inte. Detta genom att sätta in punktens koordinater i olikheterna och se om de är uppfyllda.

Ok, så kan man avrunda neråt då när man inte får x o y till heltal?

Du prövar med att avrunda x eller y neråt.

Se sedan om do kan avrunda den andra uppåt

Hej Y,

Hur sätter jag in punktens koordinater i olikheterna, har inte gjort det förut?

Ok, så ena avrundning neråt o den andra uppåt då?

Mvh/H

Henrik 2 skrev:

Hej Y,

 

Hur sätter jag in punktens koordinater i olikheterna, har inte gjort det förut?

Det beskrev jag i detta svar i en annan av dina trådar.

Ok, så ena avrundning neråt o den andra uppåt då?

Ja, om det går, dvs om punkten då fortfarande ligger i det tilååtna området.

Du vill hitta heltalsvärden på x och y som ligger nära den övre högra punkten i det tillåtna området, dvs skärningspunkten mellan y = 2x och 50x+80y = 35 000.

Fast egentligen så tror jag inte att du behöver bry dig om dessa specialfall med avrundningar.

Det troliga är att alla uppgifter du kommer att få är gjorda så att det tillåtna områdets hörnpunkter kommer att hamna på koordinater med heltalsvärden.

Hej,

Nja, jag e inte så säker på det, om man får udda tal som t ex 35 ,33 eller 37 k då blir ju y o/eller x väl inte heltal?

Mvh/H

Henrik 2 skrev:

[...]

Nja, jag e inte så säker på det,

Nej säker kan du inte vara. Men det troligaste är att uppgifterna är gjorda så att hörnpunkterna hamnar på heltalskoordinater.

Jo, det e väl så. Många tal nu som ska lösas..)

Hej,

Kikade på linjär optimering och blev lite förvirrad av detta villkor som sedan ska ställas upp som en olikhet

Villkor:

Man ska baka minst dubbelt så många y (bakelser) som x (kakor).

Olikhet

y≥2x

Stämmer det att ställa upp olikheten så?

Eller betyder denna olikhet att man ska baka minst dubbelt så många x?

Som sagt förvirrad för det ska vara den olikheten uppställd så, men blev lite förvirrad nu märkte jag när jag skulle tolka det.

Mvh/H

Henrik 2 skrev:

Hej,

Kikade på linjär optimering och blev lite förvirrad av detta villkor som sedan ska ställas upp som en olikhet

Villkor:

Man ska baka minst dubbelt så många y (bakelser) som x (kakor).

Olikhet

y≥2x

Stämmer det att ställa upp olikheten så?

Ja, det stämmer

Eller betyder denna olikhet att man ska baka minst dubbelt så många x?

Nej, $y\geq2x$ betyder "y är större än eller lika med 2x".

Ok, men blir så förvirrande för om man tar det på detta sätt.

Bakelser e 2*y och kakor e  x då man ska baka dubbelt så många y, minst. Så hänger inte riktigt med varför det ska stå som det gör i olikheten, dvs tvärtom?

Aha, nu e jag med, det betyder enbart att y= 2x eller större

Nu såg jag det o förstod det på ett annat sätt när man sätter det =.

Mvh/H

Är den här uppgiften helt klar nu eller är det något du vill att vi förklarar närmare?

Helt klar nu, sätter grön markering på den.

Mvh/H