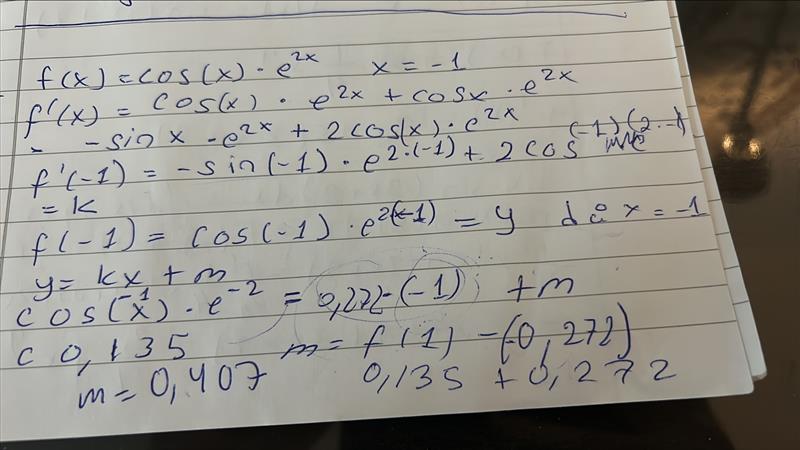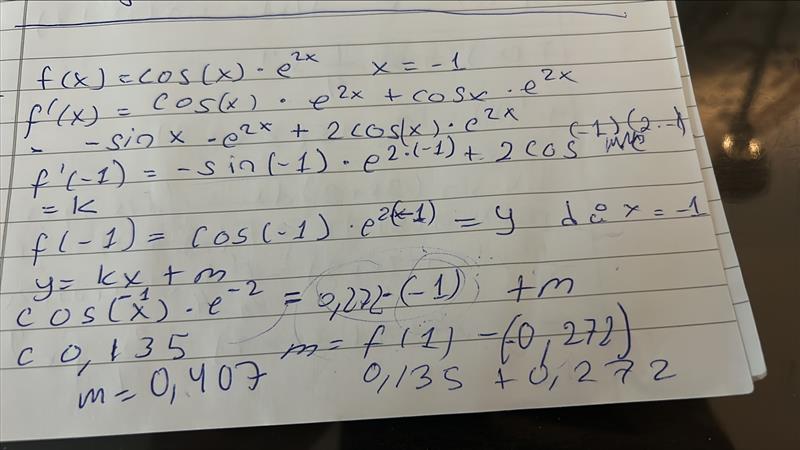linjär approximation
3.Funktionen f(x)= cos(x)*ℯ^(2x) är jobbig, gör en linjär approximation till funktionen då x=-1 (fullständig lösning krävs)
jag har löst som föjande.
Funktionen här är ett produkt av två funktioner: f(x) = g(x)h(x), där g(x) = cos(x) och h(x) = e^(2x). Vi kan använda produktregeln för derivator för att bestämma derivatan av f. Produktregeln säger att derivatan av en produkt av två funktioner är g'(x)h(x) + g(x)h'(x), där g' och h' är derivatorna av g och h.
Först bestämmer vi derivatan för varje funktion: g'(x) = -sin(x) h'(x) = 2e^(2x)
Nu kan vi använda produktregeln: f'(x) = g'(x)h(x) + g(x)h'(x) = -sin(x)*e^(2x) + cos(x)*2e^(2x)
Nu vill vi räkna ut derivatan vid punkten x=-1: f'(-1) = -sin(-1)e^(2-1) + cos(-1)2e^(2-1) = sin(1)*e^(-2) + cos(-1)*2e^(-2)
Sedan behöver vi också beräkna värdet på funktionen vid x=-1: f(-1) = cos(-1)e^(2-1) = cos(1)*e^(-2)
Så den linjära approximationen av f nära x=-1 är givet av linjen L(x) = f(-1) + f'(-1)(x - (-1)). Alltså:
L(x) = f(-1) + f'(-1)(x + 1)
Vi behöver utvärdera f(-1) och f'(-1), vilket vi har beräknat tidigare.
Vi vet att: f(-1) = cos(1)*e^(-2) f'(-1) = sin(1)*e^(-2) + cos(-1)*2e^(-2) = sin(1)*e^(-2) + cos(1)*2e^(-2)
Vårt mål är att sätta in dessa värden i vår linjära approximation.
L(x) = f(-1) + f'(-1)(x + 1) = cos(1)*e^(-2) + (sin(1)*e^(-2) + cos(1)*2e^(-2))(x + 1)
Och det är den linjära approximationen av f(x) = cos(x)*e^(2x) vid x=-1.
Snyggt, ser rätt ut. Var det något du behövde hjälp med?
ska jag sen lösa ut m genom y=kx+m?
Ja, om du vill kan du multiplicera in det beräknade f'(x) i (x+1) för att få linjen på formen y = kx +m
Calle_K skrev:Ja, om du vill kan du multiplicera in det beräknade f'(x) i (x+1) för att få linjen på formen y = kx +m
är det rätt så?
Elias.anderson skrev:Calle_K skrev:Ja, om du vill kan du multiplicera in det beräknade f'(x) i (x+1) för att få linjen på formen y = kx +m
är det rätt så?
?
Jag får lite annorlunda. Men du har ju i princip svaret redan från ditt första inlägg, bara på formen L=a+b(x+1)
Multiplicerar du in b i parentesen får du a+b + bx, därmed är b ditt k-värde och a+b är ditt m-värde.
Calle_K skrev:Jag får lite annorlunda. Men du har ju i princip svaret redan från ditt första inlägg, bara på formen L=a+b(x+1)
Multiplicerar du in b i parentesen får du a+b + bx, därmed är b ditt k-värde och a+b är ditt m-värde.
kan du skicka ditt svar
cos(1)*e^(-2) + (sin(1)*e^(-2) + cos(1)*2e^(-2)) + (sin(1)*e^(-2) + cos(1)*2e^(-2))x