Linjär algebra/trigonometri/mekanik statik
God kväll!
Övar på lite extentor och blir inte klok på detta.
Uppgiften i sig:
Tunn, homogen och kvadratisk platta på 350kg, måtten är 800mm(inte 900 som i figur). hänger horisontellt i tre rep.
Alla rep sitter fast i punkt D, 1200mm ovanför punkt G.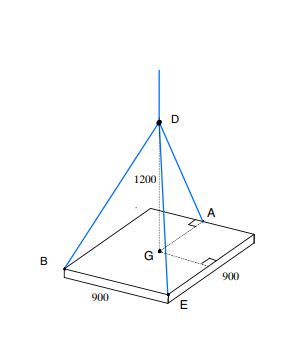
Försökte först räkna ut med vektoralgebra men kör fast och vet inte riktigt hur jag tar mig vidare.
Utgår från G som origo, skriver ner koordinaterna för A, B, D, E och G.
A: (0, 400, 0)
B: (-400, -400, 0)
D: (0, 0, 1200)
E: (400, -400, 0)
G: (0, 0, 0)
Går vidare med att räkna ut enhetsvektorerna DA, DE, DB som jag får till följande:
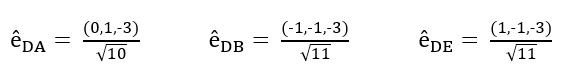Ställer sedan upp spännkrafterna, att spännkraften är ett resultat av enhetsvektorn och storleken av kraften.
Tolkar detta steg som att vi kan få fram riktningen genom att använda måtten och sen multplicera med storleken på kraften(okänd skalär?) för att få slutliga spännkraften som en vektor.
I dom exempel jag sett så byter man ordning på bokstäverna i detta steg, kan någon förklara varför?
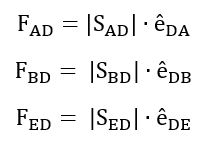
Ställer sedan upp detta som följande, alla spännkrafter ska tas ut av mg:
Nu kan jag "plocka ur" varje x, y och z.
Tydliggörs att AD inte tar upp något i x led och BD, ED tar upp lika mycket.
I y-led är BD och ED lika men AD något större.
i z-led är återigen BD och ED lika men AD något större igen.
Och här är det jag kör fast. Jag kan sätta in mg(3437 N) men ser inte hur detta hjälper mig i helhet.
Jag gissar att jag behöver ställa upp detta i en matris på något sätt och räkna ut det, men hur och vart börjar jag?
Edit 22:23, korrigerade felaktiga siffror..
Ordningen på index kan tänkas beskriva riktning "Från A till D" men jag förstår inte varför de byter. Kraftens riktning är den samma som enhetsvektorn per definition så...
Det du ska göra nu är koefficientmatris och Gaussisk radreduktion. Precis som i den matematiska grunka/grundkurs/grällen du borde läst.
Linjär algebra är väl "förstadiet" till detta, inte min starkaste kurs om vi säger så.
Gausseliminering enligt följande till trappform, tror dock mg hamnar fel?
Här kör jag dock fast igen och blir inte klok på hur jag ska tolka matrisen.
Kommer vagt ihåg att jag ska använda sista raden för att räkna ut resten men förvirringen är stor.
Dela y-raden på 12 och få ut 0 0 1 = -(mg/12) ?
Dela x-raden på 3 och få ut 0 -1 1 = 0 dvs x i sbd måste vara +(mg/12)?
Slutligen dela z-raden på 3 och få ut -1 -1 -1 = mg/3?
Symmetrin här gör att beloppen av BD och ED är lika stort. Då får du en variabel mindre i ditt ekvationssystem.
Räknade vidare och kom fram till det också, men uträkningen kan inte stämma.
Om skivan "väger" 3437N och två av tre linor, i ett relativt balanserat system, endast tar upp 86.4N var, det känns orimligt?
Edit: jag är trött och korkad. :D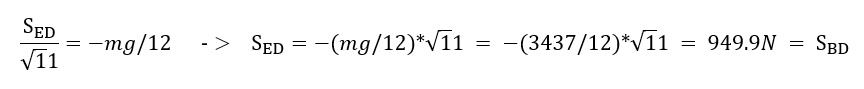
Nu ska jag bara försöka förstå hur jag ska få ut S_AD
Får dock inte ihop hur jag ska tolka matrisen.
S_ED skall då ha kolumnvektorn -1, 1, 1 men det är bara y-raden som är lika med svaret jag nyss kom fram till.
Tittar jag istället på radvektorn 1, 1, 1 = -mg/3 och ger detta värdena z: 1 + 949.9 + 949.9 = mg/3 men detta blir också bananas.
Får fortsätta imorgon men uppskattar om jag kan få en spark i rätt riktning här.
Förstår inte helt hur jag ens fick ut 949.9 utan det var nog mest tur.
Antagligen ute och cyklar men .. Om jag nu ger varje "cell" ett värde, som jag räknat ut i början med y-raden som med sitt 0 0 1 = 949.9 är självklart.
x raden blir då 0 949.9 -949.9 = 0 vilket intuitivt stämmer med att bara två rep tar upp x-krafter och x resultanten ska vara noll.
Detta får mig dock att tänka att y-raden då antyder att det finns en kraft på 949.9 i y, men detta är väl vad jag räknat ut som spännkraften i snöret dvs ED och BD. Så då blir det helt knasigt om jag har x, y, z i vänster?
Oavsett, om jag försöker samma logik på z-raden så får jag att ? + 949.9 + 949.9 = 3622.9 vilket då enligt tidigare logik borde innebära att SAD har en spännkraft på 3622.9N, men detta stämmer inte mot facit som säger 2497...
SBD och SED är negativa, du missade minustecknet i ditt svar. Du får då:
Detta blir negativt. Du har alltså gjort fel på tecken i vektordefinitionen. Dina riktningar var fel från början (krafterna i tråden kan inte komprimera dem, bara sträcka ut).
Men, detta gör inget eftersom det är ett statiskt bestämt system.
Edit: Fortfarande något som är knas tror jag. Ser inte vad på rak arm. Skulle räkna om då det är lätt att slarva.
mrcrankyface skrev:
Vi tar detta igen. Med dessa tre ekvationer får vi från X att:
Detta ger sedan med Y att:
Vilket sedan med Z ger att:
Detta blir inte 2497 N vilket måste betyda att du och facit använder olika värden. Visa en bild på facit.
Du kan superenkelt kontrollräkna med trigonometri:
Yes, efter att ha sovit på saken, och räknat om igen på flera sätt, så visar det sig att lösningen till extentan är felaktig.
Jag började försöka lösa uppgiften med trig och fick 1811N vilket inte stämde med facit, så jag förutsatte att det inte gick att använda trig på dylika problem och att jag missade någon detalj.
Har mycket bättre grepp på det hela nu, tack alla som hjälpt till!
