Linjär Algebra - Spektralsatsen

Hej!

Jag har fastnat på följande uppgift:

F : $ℝ^{3} - > ℝ^{3}$ ges i standardbasen av matrisen

A = $[\begin{matrix} 1 & 2 & 2 \\ 2 & - 2 & 1 \\ 2 & 1 & - 2 \end{matrix}]$

Ange en ON-bas för $ℝ^{3}$ bestående av egenvektorer till F. Hur kan du enkelt avgöra om
du har en höger eller vänster ON-bas?

Vad har jag gjort?

Jag kollar att A är symmetrisk. Vilket stämmer då A:s transponat är samma som A.

Sedan börjar jag med att ställa upp sekularekvationen.

$d e t (A - λ I) = 0$

Av detta får jag att $λ = 3 o c h λ = - 3 (d u b b e l r o t) ä r e g e n v ä r d e n a t i l l F .$

Jag vill nu få ut egenvektorerna så jag enligt spektralsatsen sedan kan få ut en ON bas.

För $λ = 3$ fick jag rätt egenvektor, men ej för $λ = - 3$ .

För $λ = - 3$ gjorde jag såhär:

$(\begin{matrix} 1 - (- 3) & 2 & 2 \\ 2 & - 2 - (- 3) & 1 \\ 2 & 1 & - 2 - (- 3) \end{matrix}) \underset{}{\to (\begin{matrix} 4 & 2 & 2 \\ 2 & 1 & 1 \\ 2 & 1 & 1 \end{matrix})} \to (\begin{matrix} 2 & 1 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix})$

Detta gav mig:

$x_{1} = {\frac{- s}{2}}_{} - {\frac{r}{2}}_{} x_{2} = s (s \in ℝ) x_{3} = r (r \in ℝ)$

Vilket inte ger rätt egenvektorer enligt facit.

Facit

Jag har fått ut f1, men de andra två är de som jag inte lyckats få fram.

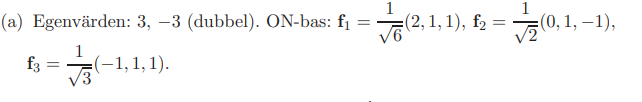
Tack på förhand!

Dina egenvektorer ser ut att stämma.

(-1/2, 1, 0) och (-1/2, 0, 1)

Men de är ju inte ortogonala med varandra.

Du måste hitta ortogonala vektorer i det här egenrummet enligt uppgiften.

jamolettin skrev:
Dina egenvektorer ser ut att stämma.

(-1/2, 1, 0) och (-1/2, 0, 1)

Men de är ju inte ortogonala med varandra.

Du måste hitta ortogonala vektorer i det här egenrummet enligt uppgiften.

Hur får jag ut ortogonala vektorer? Enligt spektralsatsen så ska det väl gå?

Japp, det går. I det här fallet ganska enkelt.

Om du adderar dina egenvektorer så får du

( - 1, 1, 1)

Om du subtraherar så får du

( 0, 1, - 1)

Och vips så har du två ortogonala.

Det är ju ingen generell metod men jag såg det bara.

Annars kan du använda Gram-Schmidt

jamolettin skrev:
Japp, det går. I det här fallet ganska enkelt.

Om du adderar dina egenvektorer så får du

( - 1, 1, 1)

Om du subtraherar så får du

( 0, 1, - 1)

Och vips så har du två ortogonala.

Ah juste. Du sa egenrummet! Det tänkte jag inte på! Nu hänger jag med :)

Förresten, kan passa på att fråga en till sak som hör till uppgiften, nämligen vad är ett lätt sätt att se om den är vänster eller höger orienterad? Hur ska man gå tillväga för att lista ut det?

Om du tar f1xf2 så ska du få f3 vid höger.

Om f1xf2 blir minus f3 så är det vänster.

(taget ur minnet, bäst du kollar upp)

jamolettin skrev:
Om du tar f1xf2 så ska du få f3 vid höger.

Om f1xf2 blir minus f3 så är det vänster.

(taget ur minnet, bäst du kollar upp)

Kryssprodukten. Aha det är så de menar. Då hänger jag med på den delen också! Tack så mycket😄

Svara

Visa senaste svar