Linjär algebra - Normalform till parameterform

Jo, det går också. Du kanske får andra vektorer, men det är inget konstigt. Ett plan kan spännas upp av två vektorer på många olika sätt.

EDIT: Nu talade jag om plan medans det handlade om linjer, jaja, det stämmer där också.

Aha, ok. Men jag tror att de vill att man ska använda formeln för normalform istället. Hur kommer jag fram till samma svar om jag använder formeln? Jag får bara fram variabler utan riktiga värden.

Jag får fram detta, men hur ska man veta att man ska sätta y = t? Varför gör man det?

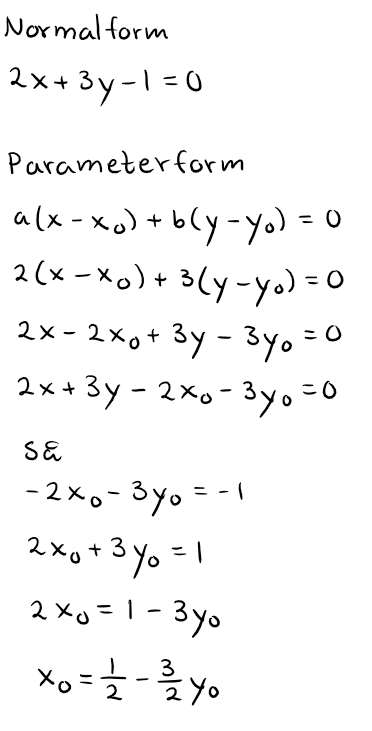
Fast $a(x-x_0)+b(y-y_0)=0$ är en linje på normalform, inte på parameterform.

En linje på parameterform använder en parameter. Det är det $t$ är.

Allmänt kan en linje skrivas på parameterform $\mathbf{a}+t\mathbf{r}$ där $\mathbf{a}$ är en punkt på linjen och $\mathbf{r}$ är linjens riktningsvektor. Om du ska få det hela på parameterform måste du någon gång introducera en parameter $t$. Om man vill kan man kalla den något annat, men du måste fortfarande bestämma vad din parameter ska vara.

Aha, ok. Nu fattar jag, tack!

I samma uppgift ska jag räkna ut riktningsvektorn, men jag fattar inte riktigt vad det är och hur man gör det. I facit står det att riktningsvektorn u = (-3/2, 1), men varför är det så? Kunde den inte ha varit (1/2, 0) istället?

Vi sa ju att linjen kunde skrivas $\mathbf{a}+t\mathbf{r}$. $\mathbf{r}$ ska ha ett $t$ framför sig och $\mathbf{a}$ ska inte ha det. Om vi skriver

$(x,y)=(1/2-3t/2,t)=(1/2,0)+t(-3/2,1)$

ser vi ju då att vi måste ha $\mathbf{a}=(1/2,0)$ och $\mathbf{r}=(-3/2,1)$, inte tvärtom.