Linjär algebra. Hur tolkar ni frågan?
Denna fråga var på min tenta igår. Den är avgörande till om jag får godkänt eller ej.
Jag tolkar den på ett sätt, men min lärare säger att den är tydlig och att det inte går att misstolka.
Hur ser ni andra på denna fråga?
OBS(innan ni tittar på min tolkning, gör er tolkning).
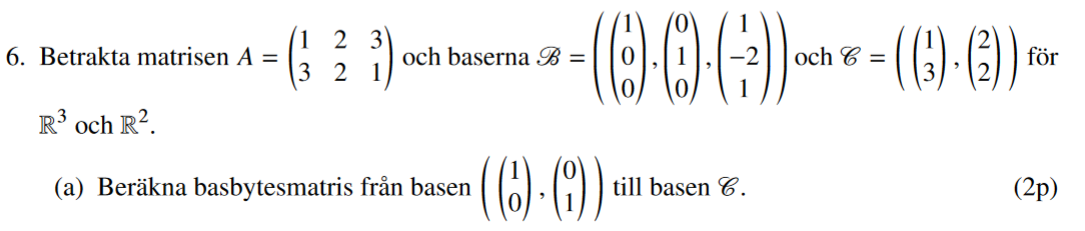
Jag tolkar att man ska ta fram P för: [x]_=cPs*[x]_s
Min lärare sa att det tydligt är p^-1 som ska tas fram. Jag håller inte med honom.
Jag tolkar frågan som att du ska hitta en matris som byter bas från standardbasen till C. Dvs. Om du har en matris/vektor i standardbasen, ska basbytesmatrisen du tar fram konvertera matrisen/vektorn till bas C.
Jag tycker också det ser ut att stå matrisen från standardbasen till och det går inte att misstolka.
Det är tråkigt att inte bli godkänd, men samtidigt är det viktigt att komma ihåg att det inte är hela världen. Alla studenter får omtentor då och då. Se det som en chans att få ett överbetyg på nästa omtenta!
Räkna igenom ett stort antal gamla tentor och gör en ordentlig genomgång av vad du behöver förbättra. En tenta är en stressig situation och för att minska den kognitiva lasten måste många saker sitta i ryggraden, annars får man lätt tidsbrist och blandar ihop allting.
Smutstvätt skrev:Jag tolkar frågan som att du ska hitta en matris som byter bas från standardbasen till C. Dvs. Om du har en matris/vektor i standardbasen, ska basbytesmatrisen du tar fram konvertera matrisen/vektorn till bas C.
Så som jag tolkade det? Eller så som läraren skrev dvs P eller p^-1?
D4NIEL skrev:Jag tycker också det ser ut att stå matrisen från standardbasen till och det går inte att misstolka.
Det är tråkigt att inte bli godkänd, men samtidigt är det viktigt att komma ihåg att det inte är hela världen. Alla studenter får omtentor då och då. Se det som en chans att få ett överbetyg på nästa omtenta!
Räkna igenom ett stort antal gamla tentor och gör en ordentlig genomgång av vad du behöver förbättra. En tenta är en stressig situation och för att minska den kognitiva lasten måste många saker sitta i ryggraden, annars får man lätt tidsbrist och blandar ihop allting.
Så du tolkar p eller p^-1? Ja men precis, det är inte hela världen. Dock skönt att slippa hamna på efterkälken igen pga dåliga och otrevliga lärare som inte kan lära ut. Allt annat hamnar ju tyvärr i kläm då.
Jag antar att den formel ni lärt er där matrisen ingår ser ut ungefär så här:
Det betyder att är den matris som för en vektor i basen till basen
Men i uppgiften vill man att du ska ta fram matrisen som utför transformationen åt andra hållet, dvs från standardbasen till basen .
Det är .
är den matris vars kolonner består av den nya basen uttryckt i den gamla" basen . Förmodligen plockade du fram under tentan. Sedan inverterade du aldrig på slutet.
Zurella skrev:Smutstvätt skrev:Jag tolkar frågan som att du ska hitta en matris som byter bas från standardbasen till C. Dvs. Om du har en matris/vektor i standardbasen, ska basbytesmatrisen du tar fram konvertera matrisen/vektorn till bas C.
Så som jag tolkade det? Eller så som läraren skrev dvs P eller p^-1?
I vilken bas är vektorerna i P skrivna, i din tolkning? Jag tolkar uppgiften som att ta fram en basbytesmatris A, sådan att .
D4NIEL skrev:Jag antar att den formel ni lärt er där matrisen ingår ser ut ungefär så här:
Det betyder att är den matris som för en vektor i basen till basen
Men i uppgiften vill man att du ska ta fram matrisen som utför transformationen åt andra hållet, dvs från standardbasen till basen .
Det är .
är den matris vars kolonner består av den nya basen uttryckt i den gamla" basen . Förmodligen plockade du fram under tentan. Sedan inverterade du aldrig på slutet.
Ja jag tog fram P, för det var så jag tolkade frågan, inte att man skulle ta fram p^-1
Smutstvätt skrev:Zurella skrev:Smutstvätt skrev:Jag tolkar frågan som att du ska hitta en matris som byter bas från standardbasen till C. Dvs. Om du har en matris/vektor i standardbasen, ska basbytesmatrisen du tar fram konvertera matrisen/vektorn till bas C.
Så som jag tolkade det? Eller så som läraren skrev dvs P eller p^-1?
I vilken bas är vektorerna i P skrivna, i din tolkning? Jag tolkar uppgiften som att ta fram en basbytesmatris A, sådan att .
Enligt vektorerna i basen C. P för: [x]_c=cPs*[x]_s
Okej, ja jag gör samma tolkning som D4NIEL, dvs att det som ska tas fram är en basbytesmatris från S till C.
Fick halvt poäng ifrån E, så bad om omprövning med 2 motivationer på andra tal, och fick godkänt :D
Dock skönt att slippa hamna på efterkälken igen pga dåliga och otrevliga lärare som inte kan lära ut.
Det var skönt att det löste sig! Men tänk på att man sällan kommer långt på att skylla på lärarna. Nu på universitetet har du ett mycket större ansvar över ditt eget lärande. Det finns oändligt med material som du kan söka fram själv eller använda andra externa källor för att lättare förstå koncept.
mrpotatohead skrev:Dock skönt att slippa hamna på efterkälken igen pga dåliga och otrevliga lärare som inte kan lära ut.
Det var skönt att det löste sig! Men tänk på att man sällan kommer långt på att skylla på lärarna. Nu på universitetet har du ett mycket större ansvar över ditt eget lärande. Det finns oändligt med material som du kan söka fram själv eller använda andra externa källor för att lättare förstå koncept.
Ehm, det är väl lärarens uppgift att se till att kunna lära ut så att man förstår samt att det finns en röd tråd genom kursen och att man väljer att utbilda sina studenter. Precis som när man går till ett företag för att köpa en bil, då förväntar man sig att säljaren informerar om det fordon man köper(även om man har ansvar att kontrollera bilen).
Ansvar är a och o och mitt andranamn. Hade jag inte tagit reda på 85% av information kring kursen på annat håll, hade jag inte ens blivit i närheten av godkänd.
Att skylla på en lärare är befogat när det finns belägg till det, dvs när man inte får den utbildning man faktiskt har rätt till, vilket tydligt framgick i kursutvärderingen och som även nämns av mina kurskamrater.
Ett annat tydligt exempel är från när vi hade en quizz i den nya kursen, envariabelanalys, i förra veckan. Jag fick Alla 4 rätt, men beror det på nuvarande kurs och lärare? NEJ! För då hade jag fått 0 rätt.
Det beror istället på min duktiga lärare på universitetet från den skola jag gick tekniskt basår på (för 2 år sedan) kombinerat med mitt egna ansvar.
Så jag anser det vara högst befogat att skylla på lärare som inte utbildar sina elever. Speciellt när jag får Höga betyg i de andra kurser som jag dessutom lägger ner mindre tid på, pga att jag hela tiden behöver lägga mer tid på mattekurserna, enbart för att leta fakta som bör vara oss till lag.
Då låter det som du har koll.
Försökte inte skydda läraren utan hjälpa dig. Baserat på min erfarenhet så borde man skaffa sig en studieteknik som är så oberoende av lärare det går (vilket du verkar lyckats med, snyggt). Man behöver utgå från att läraren är helt värdelös och att allt annat är en bonus. Under kursens gång har man liksom inte råd att lägga varken tid eller energi på dåliga lärare. Vill man göra skillnad får man väl skriva en tuff kursutvärdering:)



