Linjär Algebra - Area av parallellogram, hur ska jag tolka frågan?
Se frågan nedan:
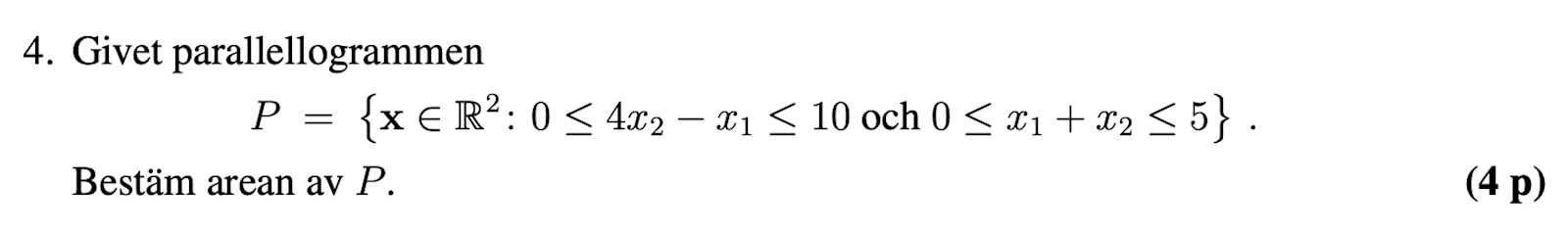
Jag har tidigare inte stött på en liknande fråga eller formulering för en figur och har svårigheter med att tolka uppgiften. Låt P vara en mängd med vektorerna x som tillhör sådana att och är det jag fattar, men inte hur jag ska visualisera mig detta, är det något form av begränsat område av ett plan eller vad är det?
Förstår inte riktigt hur jag ska tolka frågan för att påbörja en lösning.
Ersätt x1 med x och x2 med y så blir det kanske tydligare?
Yngve skrev:Ersätt x1 med x och x2 med y så blir det kanske tydligare?
Förstår faktiskt fortfarande inte, ska man ställa upp ett ekvationssystem av något slag och sedan radreducera?
Olikheterna ger dig begränsningslinjer. Försök rita in dem i ett koordinatsystem.
Börja med att anta att likhet gäller, då ger första olikheten till vänster
Hur ser den linjen ut?
Tack så mycket för hjälpen D4NIEL och Yngve! Lyckades lösa uppgiften efter att ha varit fast på den i en vecka.
Detta var det som fick mig att komma fram till lösningen:
Ersätt x1 med x och x2 med y så blir det kanske tydligare?
och
Olikheterna ger dig begränsningslinjer
Det avgörande var att inse att olikheterna kan beskrivas som fyra linjer där det instängda området är arean (vet inte varför jag inte tänkte på det med tanke på att det är gymnasienivå).
Kan lägga in min lösning här:
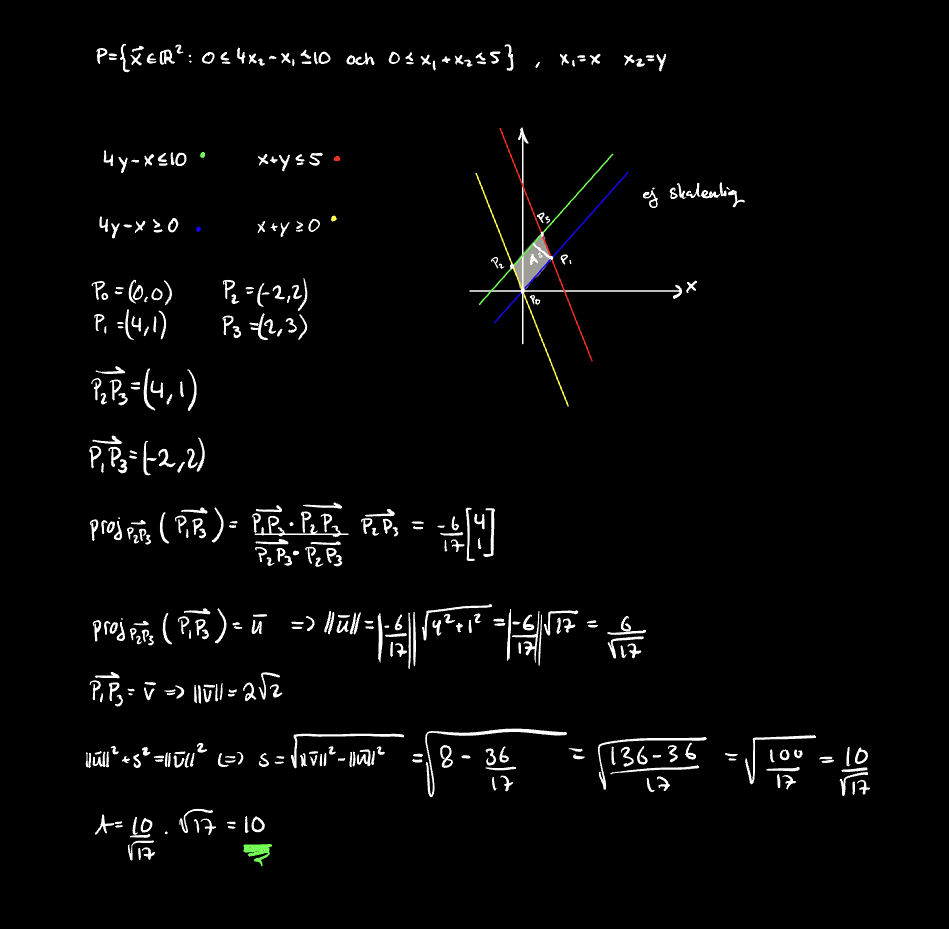
Facit har dock denna lösning:

som är snyggare och mer "linjär algebraisk" eller vad man nu ska kalla det, men förstår inte riktigt den, så om någon skulle vilja förklara hade jag uppskattat det völdigt mycket :)
De har bara gjort ett koordinatbyte
 Arean i det nya koordinatsystemet är uppenbarligen 50. Sedan kan du använda reglerna från flervariabeln, avbildningens area gånger inversen av (absolutbeloppet) av funktionaldeterminanten för transformationen (determinanten av jakobianen) är arean i det ursprungliga systemet.
Arean i det nya koordinatsystemet är uppenbarligen 50. Sedan kan du använda reglerna från flervariabeln, avbildningens area gånger inversen av (absolutbeloppet) av funktionaldeterminanten för transformationen (determinanten av jakobianen) är arean i det ursprungliga systemet.
D4NIEL skrev:De har bara gjort ett koordinatbyte
Arean i det nya koordinatsystemet är uppenbarligen 50. Sedan kan du använda reglerna från flervariabeln, avbildningens area gånger inversen av (absolutbeloppet) av funktionaldeterminanten för transformationen (determinanten av jakobianen) är arean i det ursprungliga systemet.
Har inte läst flervarren än, så förstår inte riktigt vad determinant av jakobianen eller funktionaldeterminant är , men sökte upp det och det verkade vara hur mycket ett vektorfält? stretchas i en given punkt? något sånt?
Varför behöver man den kunskapen för att lösa uppgiften som de gjort i facit?
Och koordinatbytet, har de gjort det med anledningen att beräkna area av rektangel istället för parallellogram?
Luffy skrev:Och koordinatbytet, har de gjort det med anledningen att beräkna area av rektangel istället för parallellogram?
Ja, man byter till ett koordinatsystem där figuren blir enklare. I kursen för flervariabelanalys kommer du lära dig byta till olika koordinatsystem för att förenkla area- och volymintegraler.
Det du behöver känna till för att lösa den här uppgiften på det sätt facit gör är att arean stretchas eller skalas om (som du själv påpekar) när man gör en koordinattransformation.
Det visar sig att man kan ta hänsyn till stretchningen genom att multiplicera med transformationens determinant.
Du har transformationen
Alltså behöver du multiplicera arean med en faktor för att få veta vad arean är i ditt gamla koordinatsystem.
D4NIEL skrev:Luffy skrev:Och koordinatbytet, har de gjort det med anledningen att beräkna area av rektangel istället för parallellogram?
Ja, man byter till ett koordinatsystem där figuren blir enklare. I kursen för flervariabelanalys kommer du lära dig byta till olika koordinatsystem för att förenkla area- och volymintegraler.
Det du behöver känna till för att lösa den här uppgiften på det sätt facit gör är att arean stretchas ut (som du själv påpekar) när man gör en koordinattransformation.
Det visar sig att man kan ta hänsyn till stretchningen genom att multiplicera med transformationens determinant.
Du har transformationen
Alltså behöver du multiplicera arean med en faktor för att få veta vad arean är i ditt gamla koordinatsystem.
Okej, då är jag med, tack!


