Linjär algebra, Determinant
Hej! Vilken information är väsentlig för att lösa denna uppgift? Jag är medveten om att vektorerna som kan skapas utifrån givna punkter är linjärt oberoende om determinanten inte är noll. Men bara för att vektorerna är linjärt oberoende betyder det ju inte att punkterna befinner sig i samma plan. Vad har jag missat?

Den skalära trippelprodukten kan tolkas som determinanten av den matris som har de tre vektorerna som rader eller kolonner.
Rent geometriskt är den skalära trippelprodukten volymen (med tecken) av parallellepipeden som definieras av de tre vektorerna.
Om denna volym är noll måste alla vektorer vara parallella med samma plan.
Tack! Om volymen inte är noll, dvs elementen i matrisen är linjärt oberoende, betyder detta då att ingen av dem kan befinna sig i samma plan?
Två vektorer spänner alltid ett plan genom origo med normalen om de inte är parallella.
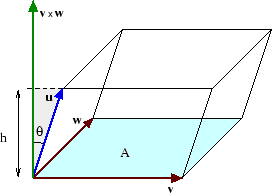 I bilden ser vi hur och spänner ett plan. Men för att parallellepipeden ska ha en nollskild volym får inte vinkeln mellan den tredje vektorn och kryssprodukten (dvs normalen till planet) vara rät. Volymen är ju determinanten
I bilden ser vi hur och spänner ett plan. Men för att parallellepipeden ska ha en nollskild volym får inte vinkeln mellan den tredje vektorn och kryssprodukten (dvs normalen till planet) vara rät. Volymen är ju determinanten
Detta klargjorde en hel del, tusen tack!


