Linjär Algebra - Bestämma planets ekvation
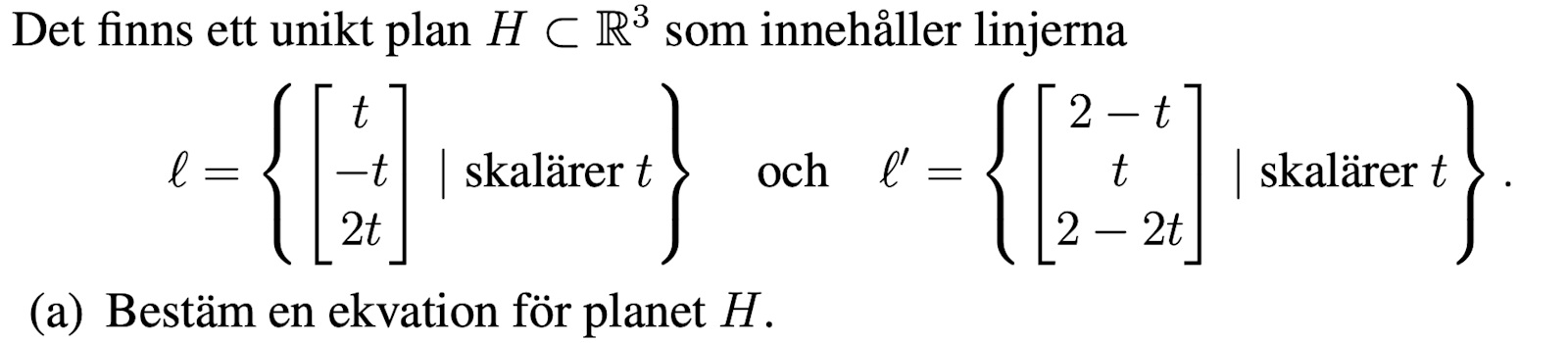
Vet inte om jag har rätt approach, men jag tänkte först att man kunde bestämma riktningsvektorerna för linjerna och sedan använda kryssprodukt på dessa för att få normalvektorn och sedan på så vis få planets ekvation på normalform. På vägen upptäckte jag däremot att dessa linjer är parallella, och jag tänkte då att man istället kan få fram en annan riktningsvektor för en annan linje men vet inte hur.
Nedan är min lösning hittills:

Skulle uppskatta lite vägledning.
Rätt men som sagt parallella linjer.
Definera en punkt på l’ och en annan på l, p’ och p.
definera nu vektor p’-p.
kryssa den med l:s riktningsvektor. Nu har du normal.
Eller hur?
Analys skrev:Rätt men som sagt parallella linjer.
Definera en punkt på l’ och en annan på l, p’ och p.
definera nu vektor p’-p.
kryssa den med l:s riktningsvektor. Nu har du normal.
Eller hur?
Hänger inte riktigt med på p' och p, är det punkterna på l' och l?
Japp!
Analys skrev:Japp!
Okej, men om man nu tar slutpunkt minus startpunkt, kommer inte den vektorn man får också vara parallell med ursprungsvektorerna?
Nej, de är ju parallella men förskjutna. testa att plugga in t =0 i båda:
p blir origo
p’ blir …
vektorn blir
…
Och nu kan du kryssa!
Analys skrev:Nej, de är ju parallella men förskjutna. testa att plugga in t =0 i båda:
p blir origo
p’ blir …
vektorn blir
…
Och nu kan du kryssa!
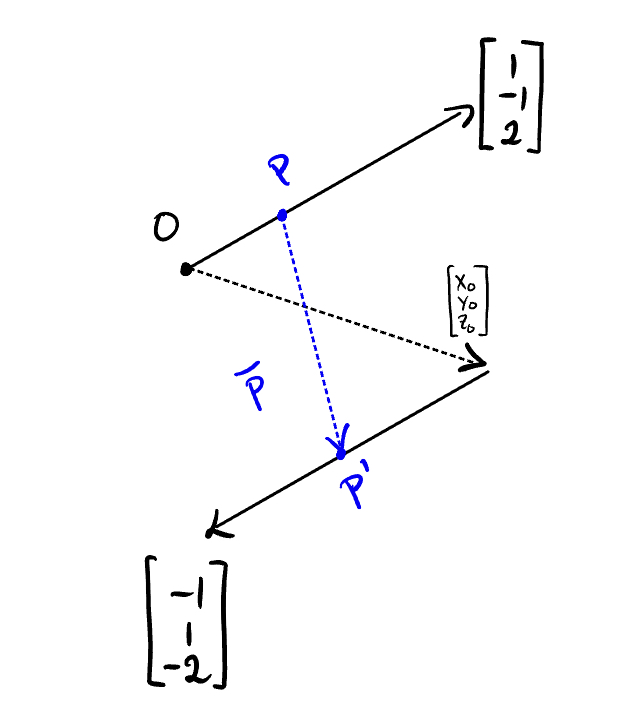
Är följande korrekt tankesätt?
P och p’ som i bilden funkar. Specifikt borde kunna ta vektor från origo till (2,0,2). Denna är ju inte paralell med riktningsvektorerna.
Verkar inte detta stämma?
Analys skrev:P och p’ som i bilden funkar. Specifikt borde kunna ta vektor från origo till (2,0,2). Denna är ju inte paralell med riktningsvektorerna.
Verkar inte detta stämma?
Jaaa okej, så man tar en vektor från origo, alltså där l börjar till punkten 2,0,2 där l' börjar?
Men visst spelar det ingen roll vart punkterna p och p' ligger på l och l' , man kommer väl fortfarande få en vektor som inte är parallell mot l och l'?
Om l' och l hade haft samma utgångspunkt och varit parallella, då hade väl det inte gått att välja en punkt p och p'?
Du har rätt att du kan välja godtyckliga punkter, du kommer då att få en vektor som också ligger planet men som inte är parallell med l och l’.
Analys skrev:Du har rätt att du kan välja godtyckliga punkter, du kommer då att få en vektor som också ligger planet men som inte är parallell med l och l’.
Okej, och om l' och l både är parallella med samma utgångsposition så kan man inte bestämma en punkt som ligger i planet eller?
Eller nej då är det ju bara samma linje bara att t är olika för vektorerna. Hänger med nu!
Tack för hjälpen! :D
Luffy skrev:Analys skrev:P och p’ som i bilden funkar. Specifikt borde kunna ta vektor från origo till (2,0,2). Denna är ju inte paralell med riktningsvektorerna.
Verkar inte detta stämma?
Jaaa okej, så man tar en vektor från origo, alltså där l börjar till punkten 2,0,2 där l' börjar?
Men visst spelar det ingen roll vart punkterna p och p' ligger på l och l' , man kommer väl fortfarande få en vektor som inte är parallell mot l och l'?
Om l' och l hade haft samma utgångspunkt och varit parallella, då hade väl det inte gått att välja en punkt p och p'?
Stämmer men då hade de varit samma linje och det hade inte funnits något unikt plan utan istället oändligt många plan som typ rollar runt linjen.

