Linjär Algebra - Bestämma ett ortogonalt plan med som skär i en bestämd linje
Hej!
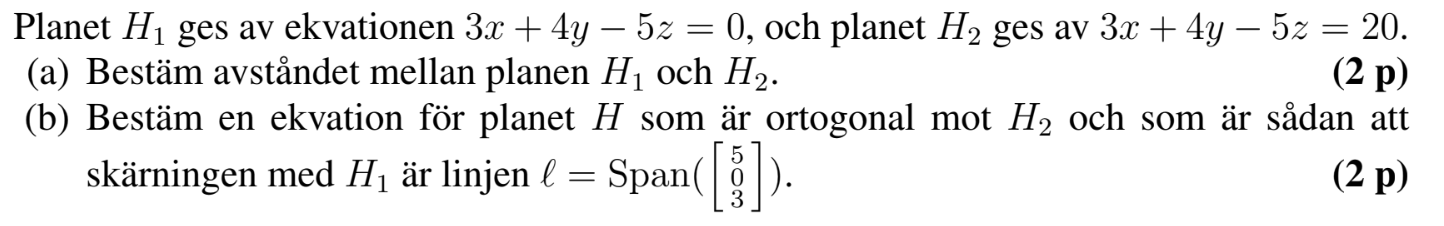
Skulle behöva hjälp på (b) uppgiften. Jag tror jag vet tankegången för uppgiften och har tänkt såhär, normalvektorn är för både och . Om man nu hittar en normalvektor till ett ortogonalt plan mot får man där är normalvektorn för planet .
Nu är ortogonalt mot men man kan ju förskjuta planet så att skärningen med blir annorlunda, men man vill att det skär på linjen .
Hur jag nu gör detta matematiskt har jag ingen aning, dvs tar fram och på något sätt får in i det hela?
Tänker jag ens rätt?
Lyckades lösa det genom att använda mig av kryssprodukt mellan normalvektor och vektorn för l om det finns någon i framtiden som läser inlägget
Nevermind, lyckades inte alls att lösa det.
Jag tänkte att man kan få normalvektorn och vektorn (5,0,3) att ligga i samma plan och sedan ta kryssprodukten av de för att få en normalvektor till planet, men det blev fel.

Varför definerar de (3,0,5) istället för (5,0,3)?
kryssning mellan normalvektorn till H2 som ingår i nya planet samt en vektor till är säkert vägen framåt.
Påminn mig, vad betyder span?
samt, de har ju använt 3 0 5 i lösningstexten men 5 0 3 i beräkningen.
Analys skrev:kryssning mellan normalvektorn till H2 som ingår i nya planet samt en vektor till är säkert vägen framåt.
Påminn mig, vad betyder span?samt, de har ju använt 3 0 5 i lösningstexten men 5 0 3 i beräkningen.
Span är alla möjliga linjär kombinationer av de givna vektorerna (så som jag förstått det).
Bisak men avståndet i a är 2*roten(2) eller hur?
men finns det nån felskriving i uppgiften och lösningen eftersom 3 o 5 skiftats?
Analys skrev:Bisak men avståndet i a är 2*roten(2) eller hur?
Yes, det stämmer
men finns det nån felskriving i uppgiften och lösningen eftersom 3 o 5 skiftats?
Vet faktiskt inte, de definerar vektorn v=(3,0,5) och sedan använder de sig av (5,0,3) så det måste väl vara fel?
Skalärprodukten mellan ”spanvektorn” och normalen till H1 blir 0. Oklart om detta för fallet framåt.
5 0 3 är ju en vektor i planet H1 som ju kan sträckas ut till en linje. Om det är denna som avses så är ju kryssprodukten mellan denna och H2s normal noramlen till det nya planet H3 och dörmed plankoefficienter framför x,y,z.
Analys skrev:5 0 3 är ju en vektor i planet H1 som ju kan sträckas ut till en linje. Om det är denna som avses så är ju kryssprodukten mellan denna och H2s normal noramlen till det nya planet H3 och dörmed plankoefficienter framför x,y,z.
Yes, jag håller med, får dra slutsatsen att det är fel i facit.
Det är inte fel i facit (eller ja, de har tydligen råkat skriva (3,0,5) på ett ställe, men rättar sig genast på nästa rad till (5,0,3)
Normalen till det sökta planet ska vara ortogonal mot normalen till samt ortogonal mot varje vektor som ligger i . Eftersom är en vektor i kan man alltså studera kryssprodukten
Ett annat (omständligare) sätt att uttrycka det är att normalen till ska uppfylla
Facits svar är en korrekt ekvation för det sökta planet

