Linjär algebra, bestäm avbildningsmatrisen för spegling
Jag har problem med denna uppgiften, jag får inte fram rätt svar.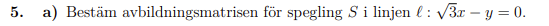
Svaret ska bli:
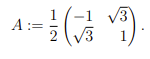
Min uträkning är: Jag har gjort två uträkningar där den första ger rätt svar MEN den innehåller ett fel som jag har ringat in och den andra uträkningen ger det svar som borde vara rätt?
Jag har gjort två uträkningar där den första ger rätt svar MEN den innehåller ett fel som jag har ringat in och den andra uträkningen ger det svar som borde vara rätt?
Så det jag undrar över är om det är del i facit eller har jag missat något? Tack på förhand :)
n och v som du bestämmer i första lösningen är inte ortogonala.
Calle_K skrev:n och v som du bestämmer i första lösningen är inte ortogonala.
v skrev jag ut för att testa en tanke, som inte ledde mig vidare, och sen fick den stå kvar. Men jag använde inte v i min uträkning.
Du kan testa punkten (, -1).
Laguna skrev:Du kan testa punkten (, -1).
Kan du utveckla vad du menar att jag ska testa?
Punkten är den punkt jag har använt mig av när jag tog fram avbildningsmatrisen.
Vad avbildas den på? De båda matriserna ger olika resultat.
Laguna skrev:Vad avbildas den på? De båda matriserna ger olika resultat.
Den avbildas på linjen och vektorn (√3,−1) är den vektorn som är ortogonal mot linjen.
Det jag behöver hjälp med är att förstå om det är jag som har räknat fel eller om det är facit som är fel.
Nej, den avbildas inte på linjen. Jag tog den för att det är lätt att räkna ut i huvudet vad den avbildas på av de båda matriserna. Den ena ger rätt svar, nämligen facits, så det är nog inte fel i facit. Det är allt jag har kollat på, så jag vet inte precis vad som gick fel hos dig.
Laguna skrev:Nej, den avbildas inte på linjen. Jag tog den för att det är lätt att räkna ut i huvudet vad den avbildas på av de båda matriserna. Den ena ger rätt svar, nämligen facits, så det är nog inte fel i facit. Det är allt jag har kollat på, så jag vet inte precis vad som gick fel hos dig.
Ok tack :)
Då betyder det att min första uträkning är rätt men jag har på nått sätt kastat om ett tecken innan jag räknade fram avbildningsmatrisen.
Robin2518 skrev:Laguna skrev:Nej, den avbildas inte på linjen. Jag tog den för att det är lätt att räkna ut i huvudet vad den avbildas på av de båda matriserna. Den ena ger rätt svar, nämligen facits, så det är nog inte fel i facit. Det är allt jag har kollat på, så jag vet inte precis vad som gick fel hos dig.
Ok tack :)
Då betyder det att min första uträkning är rätt men jag har på nått sätt kastat om ett tecken innan jag räknade fram avbildningsmatrisen.
Tror att jag har löst den nu, men jag har fått vektorerna i fel ordningen, enligt facit, men det kanske inte spelar någon roll?
Det är nog underförstått att de vill se standardmatrisen för avbildningen. Dvs matrisen relativt standardbasen (E): e1 = (1 0)T, e2 = (0 1)T.
Om vi tänker oss en bas F bildad av dina normerade vektorer n och v så ges matrisen för speglingen relativt denna bas av
[S]F = .
Matrisen relativt standardbasen ges då mha basbytesmatriser av
[S]E = PF->E[S]FPE->F.
PF->E = , PE->F = (PF->E)T.
PATENTERAMERA skrev:Det är nog underförstått att de vill se standardmatrisen för avbildningen. Dvs matrisen relativt standardbasen (E): e1 = (1 0)T, e2 = (0 1)T.
Om vi tänker oss en bas F bildad av dina normerade vektorer n och v så ges matrisen för speglingen relativt denna bas av
[S]F = .
Matrisen relativt standardbasen ges då mha basbytesmatriser av
[S]E = PF->E[S]FPE->F.
PF->E = , PE->F = (PF->E)T.
Tack för att du tog dig tid att svara :)
Jag för står inte riktigt hur du kom fram till detta med? tänker framför allt på " -1 "
Sedan är jag också fundersam över det som jag kom fram till
När det i facit står
Är detta samma sak? eftersom att den ända skillnaden är att kolonnerna har bytt plasts? eller har jag missuppfattat något?
Om du speglar normalen n i linjen så får du -n. Om du speglar v i linjen så får du v, eftersom v är parallell med linjen.
Matrisen [S]F har koordinaterna för bilderna av basvektorerna som kolonner. Koordinaterna för -n i basen F är (-1 0)T och för v är de (0 1)T. Så det förklarar utseendet på [S]F.
Jag förstår inte riktigt hur du får fram din matris S.
Du skriver = S-1E. Vad menar du med detta? Hur får du fram S-1?




