Linjär algebra. Beräkna e2 x (2e1 - e2 + 3e3)

Hej, jag skulle behöva hjälp med följande uppgift:

Beräkna e₂ x (2e₁ - e₂ + 3e₃)

Jag har lyckats förenkla uttrycket till det här:

(e₂ x e₁)2-(e₂ x e₃)3 = ...

Sedan vet jag inte hur jag ska göra.
Jag vet visserligen att det finns ett schema med e₁ x e₂ = -e₃ och med e₂ x e₃ = e_1,men jag förstår inte varför det blir så.

Det som jag tror mig veta är att tre vektorer sägs vara positivt orienterade om den minsta vridning som överför den första i den andra sett från spetsen av den tredje sker moturs, och negativt orienterade om den minsta vridning som överför den första i den andra sker medurs sett från spetsen av den tredje.

Och att det finns en högerhands-regel man kan använda men jag förstår inte riktigt hur man gör?

Högerhandsregler finns det många av, kanske kan den här vara tydlig:

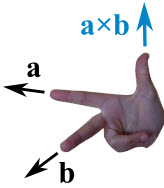
Det viktigt att lägga märke till uppräkningsordningen av basvektorerna (1,2,3)

Om de är högerorienterade och man räknar upp dem i rätt ordning (jämn permutation) är svaret positivt.

$\mathbf{e}_1\times\mathbf{e}_2=\mathbf{e}_3$ (1,2,3)

$\mathbf{e}_2\times\mathbf{e}_3=\mathbf{e}_1$ (2,3,1)

$\mathbf{e}_3\times\mathbf{e}_1=\mathbf{e}_2$ (3,1,2)

Om vi däremot räknar upp dem i fel ordning (udda permutation) blir svaret negativt

$\mathbf{e}_1\times\mathbf{e}_3=-\mathbf{e}_2$ (1,3,2)

$\mathbf{e}_2\times\mathbf{e}_1=-\mathbf{e}_3$ (2,1,3)

$\mathbf{e}_3\times\mathbf{e}_2=-\mathbf{e}_1$ (3,2,1)

I ditt exempel har du

$\mathbf{e}_2\times(2\mathbf{e}_1-\mathbf{e}_2+3\mathbf{e}_3)$

$2\mathbf{e}_2\times \mathbf{e}_1+3\mathbf{e}_2\times\mathbf{e}_3$

$-2\mathbf{e}_3+3\mathbf{e}_1$

Jag tror att jag förstår nu, tack så mycket!

Svara