Linjär Algebra - Beräkna area av parallellogram
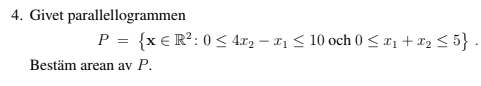
Hejsan,
Jag förstår verkligen inte alls hur jag ska kunna lösa den här uppgiften. De formler vi har lärt oss för att beräkna area av en parallellogram involverar alltid att man ska kunna skriva parallellogrammen på parameterform och sedan ta kryssprodukten av riktningsvektorerna men jag vet inte hur man skulle kunna gå från den nuvarande beskrivningen till det. Jag vet inte heller om det finns något slags trick att beräkna arean som jag inte känner till än som hade kunnat vara användbart här.
Mycket tacksam för svar!
Om du vet hörnpunkterna, kommer du vidare då?
Området är skrivet som två uppsättningar parallella linjer ax+by+c=0, med varierande c.
Det ger två "band" i xy-planet, och det sökta området är där "banden" överlappar.
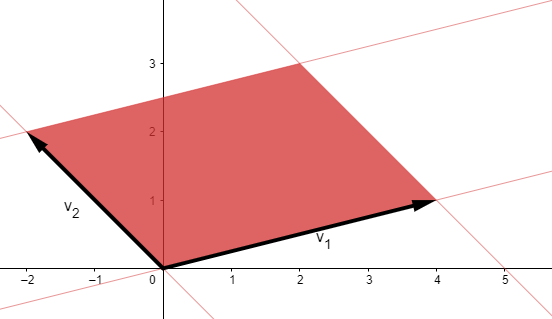
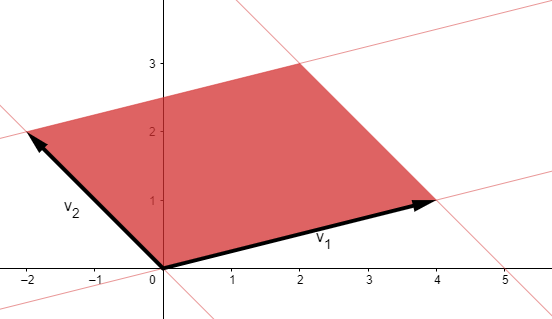
Om du ritar området kan du se att vektorerna som spänner upp det ges av:
Se nedan bild:
Tack för att ni har svarat, ursäkta att jag upptäckte det lite sent.
Jag kan inte förstå hur jag kan hitta hörnpunkterna men om jag hade kunnat finna dem hade jag löst uppgiften. Jag antar att Ebola har använt sig av hörnpunkterna för att kunna definiera riktningsvektorerna men jag fattar liksom inte hur man ska komma fram till just hörnen.
10 = 4x2 - x1
5 = x1 + x2
ger ett hörn, t.ex.
Borde jag alltså skapa 4 separata ekvationssystem där jag söker lösning för de fyra olika kombinationerna man kan skapa av gränserna till intervallen? Och varje lösning till respektive ekvationssystem kommer korrespondera mot ett hörn av parrallellogrammet?
Alltså:
10 = 4x2 - x1
5 = x1 + x2
för hörn 1
0 = 4x2 - x1
5 = x1 + x2
för hörn 2
0 = 4x2 - x1
0 = x1 + x2
för hörn 3
10 = 4x2 - x1
0 = x1 + x2
för hörn 4
Jag ser att detta fungerar och ger de hörn som är korrekta, finns det någon enkel/intuitiv förklaring till varför?
Gränserna är fyra parvis parallella linjer. Där linjerna korsar varandra är hörnen.
Om det hade varit fyra godtyckliga linjer (ej parallella) så hade det blivit fler skärningspunkter, och då får man fundera på vilka skärningspunkter som faktiskt ligger på randen.
Om du tittar på Ebolas bild i inlägg #4, är det då något som skiljer den här uppgiften från dina tidigare?
Inte säker på vad du menar
Ebola skrev:Om du ritar området kan du se att vektorerna som spänner upp det ges av:
Se nedan bild:
Kan du skriva linjerna v1 och v2 på parameterform?
Absolut, det enda jag inte förstod var hur jag skulle finna hörnen av parallellogrammen när den var skriven med linjära olikheter, alltså hur jag skulle finna v1 och v2
Midnattsmatte skrev:Absolut, det enda jag inte förstod var hur jag skulle finna hörnen av parallellogrammen när den var skriven med linjära olikheter, alltså hur jag skulle finna v1 och v2
Som vanligt - rita!
Förlåt för att det låter som att jag bara skriver massa frågor utan att försöka men mitt problem hela tiden med denna uppgift är att jag helt inte förstår hur jag ska kunna dra några som helst slutsatser om vilka x1 och x2 värden som uppfylls och därmed inte kan rita någonting alls - det är liksom det som är mitt problem från grunden.
Jag kallar x1 för x och x2 för y, för det tycker jag är enklare. Området begränsas av fyra linjer:
4y-x = 0 => y = x/4
4y-x = 10 => y = x/4 + 5/2
x+y = 0 => y = -x
x+y = 5 => y = -x+5
Visst kan du rita upp de linjerna i ett koordinatsystem?
Ok, så när en geometrisk figur beskrivs på detta sätt med olikheter så är det alltså olikheternas gränsvärden man ska utgå ifrån när man vill finna linjerna som utgör "ramen" för figuren?
Ja, precis som på gymnasiet.
Ok, tack så mycket!

.jpg?width=80&crop=0,0,80,80)