Linjär Algebra - Andragradskurvor/ytor

Hej!

Jag ska ange de punkter på ytan som ligger närmast origo och, om sådana
finnes, de som ligger längst ifrån.

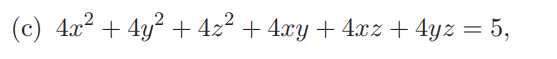
Från början så ställde jag upp $X^{t} A X d ä r A = [\begin{matrix} 4 & 2 & 2 \\ 2 & 4 & 2 \\ 2 & 2 & 4 \end{matrix}]$ . Jag använde mig av sekularekvationen på A och fick ut egenvärden. Jag hittade sedan egenvektorer för respektive värde och använde mig av dessa för att skapa en bas

$f = (\frac{1}{\sqrt{6}} (\begin{matrix} \sqrt{2} \\ \sqrt{2} \\ \sqrt{2} \end{matrix}) \frac{1}{\sqrt{6}} (\begin{matrix} - 2 \\ 1 \\ 1 \end{matrix}) \frac{1}{\sqrt{6}} (\begin{matrix} 0 \\ \sqrt{3} \\ \sqrt{3} \end{matrix}))$ . Vektorerna är förlängda så alla har samma koefficient.

Vi kan nu skapa $T o c h T^{t} . T = \frac{1}{\sqrt{6}} [\begin{matrix} \sqrt{2} & - 2 & 0 \\ \sqrt{2} & 1 & \sqrt{3} \\ \sqrt{2} & 1 & - \sqrt{3} \end{matrix}], T^{t} = t r a n s p o n a t e t a v T = i n v e r s e n a v T .$

Vi får nu att Q(fX) = $T^{t} A T$ (där f är den nya basen) = $8 x^{2} + 2 x^{2} + 2 z^{2} = 5$

Det här är en ellipsoid, vilket det ska vara. Men hur vet man om ekvationen ovan stämmer? Varför gör man en ny bas och omvandlar A till den basen?

Nu kommer vi till den delen där jag inte riktigt vet hur jag ska gå tillväga. Vi ska hitta minsta respektive längsta avståndet ifrån origo. Jag antar att vi ska använda formeln:

$^{λ_{m i n} {|u|}^{2} \leq Q (u) \leq λ_{m a x} {|u|}^{2}}$ , men jag vet inte hur man ska tänka när man använder den. Finns exempel där min professor använt den, men han hoppade extremt många steg. Hur ska man lösa avståndsdelen?

För att underlätta för er så har facit gett:

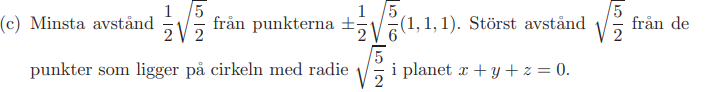
Tack på förhand!

Du byter bas för att kunna rita upp den och kolla en axel i taget.

Tex avstånd på ny x-axel blir 8x^2=5 och avstånd på y eller z-axel blir 2y^2=5.

Micimacko skrev:
Du byter bas för att kunna rita upp den och kolla en axel i taget.

Tex avstånd på ny x-axel blir 8x^2=5 och avstånd på y eller z-axel blir 2y^2=5.

Okej, smart. Hur skiljer man på ytor och kurvor? Är det så att ytor har x,y,z medan kurvor har x,y?

Även här kan man klara sig utan linjär algebra om man skulle vilja det.

$x^{2} + y^{2} + z^{2} + x y + y z + z x = \frac{5}{4} \Rightarrow x^{2} + y^{2} + z^{2} = \frac{5}{4} - (x y + y z + z x) \geq {x y + y z + z x = \frac{2 (x^{2} + y^{2} + z^{2}) - ({(x - y)}^{2} + {(y - z)}^{2} + {(z - x)}^{2})}{2} \leq x^{2} + y^{2} + z^{2}} \geq \frac{5}{4} - (x^{2} + y^{2} + z^{2}) \Rightarrow x^{2} + y^{2} + z^{2} \geq \frac{5}{8} x^{2} + y^{2} + z^{2} + x y + y z + z x = \frac{5}{4} \Rightarrow x^{2} + y^{2} + z^{2} = \frac{5}{4} - (x y + y z + z x) \leq {x y + y z + z x = \frac{{(x + y + z)}^{2} - (x^{2} + y^{2} + z^{2})}{2} \geq - \frac{x^{2} + y^{2} + z^{2}}{2}} \leq \frac{5}{4} + \frac{x^{2} + y^{2} + z^{2}}{2} \Rightarrow \frac{x^{2} + y^{2} + z^{2}}{2} \leq \frac{5}{4} \Rightarrow x^{2} + y^{2} + z^{2} \leq \frac{5}{2}$

henrikus skrev:
Även här kan man klara sig utan linjär algebra om man skulle vilja det.

$x^{2} + y^{2} + z^{2} + x y + y z + z x = \frac{5}{4} \Rightarrow x^{2} + y^{2} + z^{2} = \frac{5}{4} - (x y + y z + z x) \geq {x y + y z + z x = \frac{2 (x^{2} + y^{2} + z^{2}) - ({(x - y)}^{2} + {(y - z)}^{2} + {(z - x)}^{2})}{2} \leq x^{2} + y^{2} + z^{2}} \geq \frac{5}{4} - (x^{2} + y^{2} + z^{2}) \Rightarrow x^{2} + y^{2} + z^{2} \geq \frac{5}{8} x^{2} + y^{2} + z^{2} + x y + y z + z x = \frac{5}{4} \Rightarrow x^{2} + y^{2} + z^{2} = \frac{5}{4} - (x y + y z + z x) \leq {x y + y z + z x = \frac{{(x + y + z)}^{2} - (x^{2} + y^{2} + z^{2})}{2} \geq - \frac{x^{2} + y^{2} + z^{2}}{2}} \leq \frac{5}{4} + \frac{x^{2} + y^{2} + z^{2}}{2} \Rightarrow \frac{x^{2} + y^{2} + z^{2}}{2} \leq \frac{5}{4} \Rightarrow x^{2} + y^{2} + z^{2} \leq \frac{5}{2}$

Tyvärr så måste vi använda oss av de begrepp vi lärt oss inom linjär algebra. Tack ändå!

En kurva har en dimension, och en yta 2. För varje ekvation som beskriver området brukar man normalt sett bli av med en dimension.

Så i 3d med en ekvation har du en yta, två ekvationer ger en kurva och 3 ekvationer en punkt.

Micimacko skrev:
En kurva har en dimension, och en yta 2. För varje ekvation som beskriver området brukar man normalt sett bli av med en dimension.

Så i 3d med en ekvation har du en yta, två ekvationer ger en kurva och 3 ekvationer en punkt.

Hänger inte riktigt med, den ekvationen jag fick är väl 3d då den har x, y och z?

Ja då får vi anta att du är i ett 3d-rum. Och du har bara en ekvation som beskriver området, så det är en yta.

Micimacko skrev:
Ja då får vi anta att du är i ett 3d-rum. Och du har bara en ekvation som beskriver området, så det är en yta.

Hur skulle man kunna gå tillväga när man ska lista ut minsta/största avståndet på ytan ifrån origo? Vet ej hur man ska använda formeln i det sammanhanget.

Det var ju det jag visade högre upp. Efter att ha bytt till en bas så att alla halvaxlar till ellipsen ligger på de vanliga xyz-axlarna kan du bara testa en variabel i taget genom att sätta de andra 2 till 0 och lösa ekvationen för att få ut avståndet.

Micimacko skrev:
Det var ju det jag visade högre upp. Efter att ha bytt till en bas så att alla halvaxlar till ellipsen ligger på de vanliga xyz-axlarna kan du bara testa en variabel i taget genom att sätta de andra 2 till 0 och lösa ekvationen för att få ut avståndet.

(Är på mobilen så mitt svar är ej formaterat korrekt)

Jag gjorde som du sa och får z = +-sqrt(5/2). I facit får de inte det svaret. z eller y har ju det kortaste avståndet till origo? Har jag fattat något fel?

är det inte lättast att använda lagrange multiplikatorer?

ItzErre skrev:
är det inte lättast att använda lagrange multiplikatorer?

Har inte hört talats om det

MatteLiam skrev:
Micimacko skrev:
Det var ju det jag visade högre upp. Efter att ha bytt till en bas så att alla halvaxlar till ellipsen ligger på de vanliga xyz-axlarna kan du bara testa en variabel i taget genom att sätta de andra 2 till 0 och lösa ekvationen för att få ut avståndet.

(Är på mobilen så mitt svar är ej formaterat korrekt)

Jag gjorde som du sa och får z = +-sqrt(5/2). I facit får de inte det svaret. z eller y har ju det kortaste avståndet till origo? Har jag fattat något fel?

Du får kortaste avstånd längs x-axeln och längsta i yz-planet. (Om du använder dig av 8x^2+2y^2+2z^2=5) så det ser ut som du gör rätt.

och längsta avstånd på en cirkel

Svara

Visa senaste svar