Linjär algebra
Jag hade en fråga om den här uppgiften. Jag förstår att man får ut matrisen utifrån ekvationssystemet, men jag förstår inte hur man utför steget -R1 + R2 och hur man kommer fram till den slutliga matrisen?
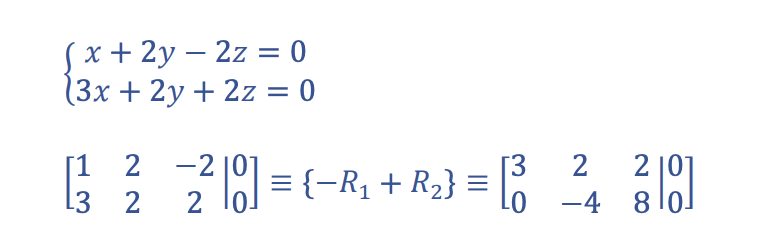
Chemengin skrev:Jag hade en fråga om den här uppgiften. Jag förstår att man får ut matrisen utifrån ekvationssystemet, men jag förstår inte hur man utför steget -R1 + R2 och hur man kommer fram till den slutliga matrisen?
Jag tror de har glömt att skriva att de har multiplicerat 3 med rad 1 och addera det till rad 2. Matrisen längst till höger är resultatet på radoperationen
Om du säger multiplicerat -3 så håller jag med. Bra kommentar.
Idén verkar vara att få 0 nere till vänster, men -R1+R2 är inte alls det de gör.
Okej, så hur får man fram 3 i första raden? Man tar -3 multiplicerat med 1 (alltså -3) plus 3, vilket blir 0. Men det är ju 3 som står först i raden i den slutliga matrisen. Eller räknar jag fel?
Hm, de verkar också ha flyttat upp andra raden så den blir första raden.
Okej, så hur skulle uträkningen se ut för 3 i den slutliga matrisen? Förstår inte hur det blir 3.
Första raden är R2.
Andra raden är -3R1+R2.
Jaha, okej. Nu fattar jag, tack!
Tänkte också fråga, varför har man ett likhetstecken med tre streck? Vad betyder det exakt?
Jag vet inte vad de menar, faktiskt. Man får skriva lite mer för att visa vad man gör, tycker jag.
Okej, det står tyvärr inget mer om det i facit.
Men jag hade också en annan fråga. Hur kom man fram till att man ska köra -3R1+R2 för andra raden och är det alltid så att första raden i den ursprungliga matrisen också blir den första raden i den slutliga matrisen?
När man gör Gauss-elimination brukar man gå neråt rad för rad, och i varje steg subtrahera så många gånger av en rad från nästa rad så att första termen försvinner. För att få bort 3:an i början av andra raden subtraherar man 3 gånger första raden.
Varför de inte låter första raden vara som den är vet jag inte. Något om det borde stå i din kurslitteratur.
Så alltså vill man att den första termen i den första raden ska bli 0?