Linjär Algebra - 7.23
Låt pi vara planet genom punkterna P:(1, 0, 2), Q:(1, 1, 4) och origo. Bestäm avbildningsmatrisen för den linjära avbildningen som svarar mot spegling i pi.
Kan du bestämma planets normalvektor?
Dr. G skrev:Kan du bestämma planets normalvektor?

n=(-2, -2, 1)**
Ja, tror de finns någon formel för just spegling i planet men fick inte det förväntade svaret. Har testat S(u)=u*(u*n/n*n)*n där u är en punkt i planet som ex. (1, 0, 2) och n är normalvektor.
Normalvektorn är t.ex
(2, 2, -1)
Du kan antingen lösa ett ekvationssystem eller kryssa OP x OQ.
För spegling så kan du först ta fram matrisen för projektion på normalvektorn (genom att projicera de tre basvektorerna på normalen).
34shuno skrev:Ja, tror de finns någon formel för just spegling i planet men fick inte det förväntade svaret.
Det finns en formel för spegling i plan som borde ge rätt svar om inte räknat fel och använt rätt formel:)
Tycker personligen däremot att det är bättre att förstå vad formlerna gör rent geometriskt så man slipper memorera.
Här har jag ritat upp ett plan samt en godtycklig vektor. Jag har även delat upp denna vektor i två delar: en som är vinkelrät mot planet och ett som är paralellt med (ligger på) planet:

Om du kollar på denna bild, tror du att du skulle kunna lista ut ifrån geometrisk vektoraddition hur du kommer från v till ref(v)? Om du sedan kommer fram till det sambandet (som är reflektionsformeln för vektorer i plan) och räknar ut det för respektive basvektor, så borde du få rätt:)
coffeshot skrev:34shuno skrev:Ja, tror de finns någon formel för just spegling i planet men fick inte det förväntade svaret.
Det finns en formel för spegling i plan som borde ge rätt svar om inte räknat fel och använt rätt formel:)
Tycker personligen däremot att det är bättre att förstå vad formlerna gör rent geometriskt så man slipper memorera.
Här har jag ritat upp ett plan samt en godtycklig vektor. Jag har även delat upp denna vektor i två delar: en som är vinkelrät mot planet och ett som är paralellt med (ligger på) planet:
Om du kollar på denna bild, tror du att du skulle kunna lista ut ifrån geometrisk vektoraddition hur du kommer från v till ref(v)? Om du sedan kommer fram till det sambandet (som är reflektionsformeln för vektorer i plan) och räknar ut det för respektive basvektor, så borde du få rätt:)
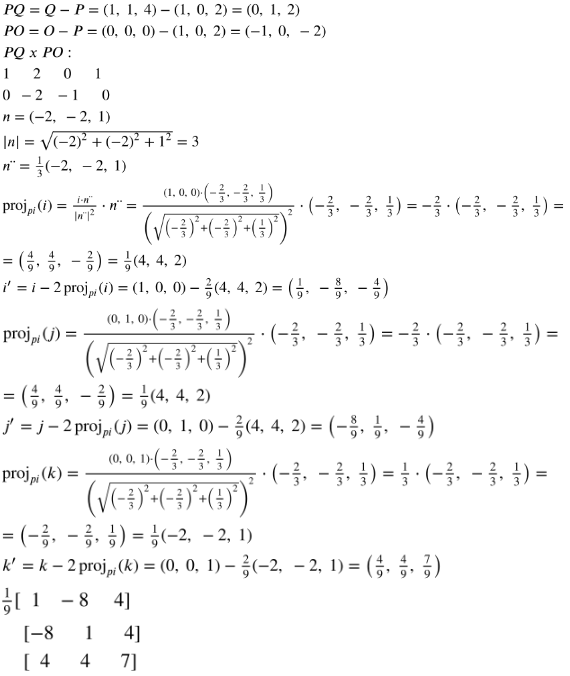
Jag tror jag löste de, postar svaret här för framtida användare. Tack så mycket för all hjälp !!


