line-voltage

$u_{n3}=1000\angle 240$

Det kanske finns andra "trefas-knep" än att rå-räkna, men om det finns så har jag isåfall glömt bort dem.

Teckna linjespänningarna (räkna om den till komplex representation, eller kanske jomega)

$u_{n1}=1000\angle 0$

$u_{n2}=1000\angle \frac{2\pi }{3}$

$u_{n3}=1000\angle \frac{4\pi }{3}$

sedan 

$Z_n=0.2+2j$

$Z_l=30$

och räkna ut strömmarna som går genom respektive impedanser $Z_l$ mellan faserna, dvs $i_{12}, i_{23} och i_{31}$etc. Sedan räkna ut spänningarna över $Z_n$ etc. Jobbigt, men just jag ser inget annat sätt. Försök en stund, om ingen annan nappar på din fråga.

Tack snälla, ska testa med det!

Såhär ser min lösning ut hittills men jag undrar hur jag ska få spänningen till endast ett tal och inte med en vinkel. Dessutom när jag räknar ut spänningarna blir de väldigt höga och orealistiska.

Ett fel som du gör är att de definierade strömmarna $i_{12}, i_{23} och i_{31}$är de strömmar som går genom lastimpedansen $30\Omega$. De strömmar som kommer att gå i respektive fas genom ledningsimpedansen $Z_n$är i tur och ordning $i_{12}-i_{31}, i_{23}-i_{12} och i_{31}-i_{23}$(kirchoffs strömlag). Och sedan måste du potentialvandra (kirchoffs spänningslag) från ena linjespänningen till den andra, på tre ställen, för att få tre olika ekvationer för att kunna beräkna de tre strömmarna.

Prydliga uträknar, det är enkelt att följa med, men gör en figur med strömmarna inritade också, annars blir det nästan hopplöst att använda kcl och kvl.

Jag hänger inte riktigt med kring hur strömmarna ska gå. Dock känns det som att lösningen är svårare än vad den behöver vara. Ett förslag på lösning ger de (se nedan), men den underlättar inte för mig.

Leona11 skrev:

Jag hänger inte riktigt med kring hur strömmarna ska gå. Dock känns det som att lösningen är svårare än vad den behöver vara. Ett förslag på lösning ger de (se nedan), men den underlättar inte för mig.

Det är typ det där jag menar med "trefas-knep". Jag kan tyvärr inte hjälpa dig med det, men det lär bli 3ggr så få beräkningar.

Jag ska testa och räkna lite senare, iallafall lägga upp en bild.

Jag förstår. Tack för hjälpen iallafall.

Jag gjorde en figur med hur jag skulle räkna om jag inte hade vetat att man kunde ta genvägar. (Jag har inte räknat, bara ställt upp). Spänningsdelning mellan linjeimpedansen och lastimpedansen för alla tre faserna. Det blir jobbigt att räkna, men är fullt möjligt.

Att man kan ta genvägar i detta fall låter rimligt, eftersom alla laster är symmetriska. Det ser ut att finnas lite om enfasekvivalent krets på youtube (och det borde finnas i din lärobok eller kompendium). Ska titta lite på det imorgon kväll om jag får tid. Man lär sig nya grejer hela tiden.

Jag tror jag hittat lite användbara trefasknep:

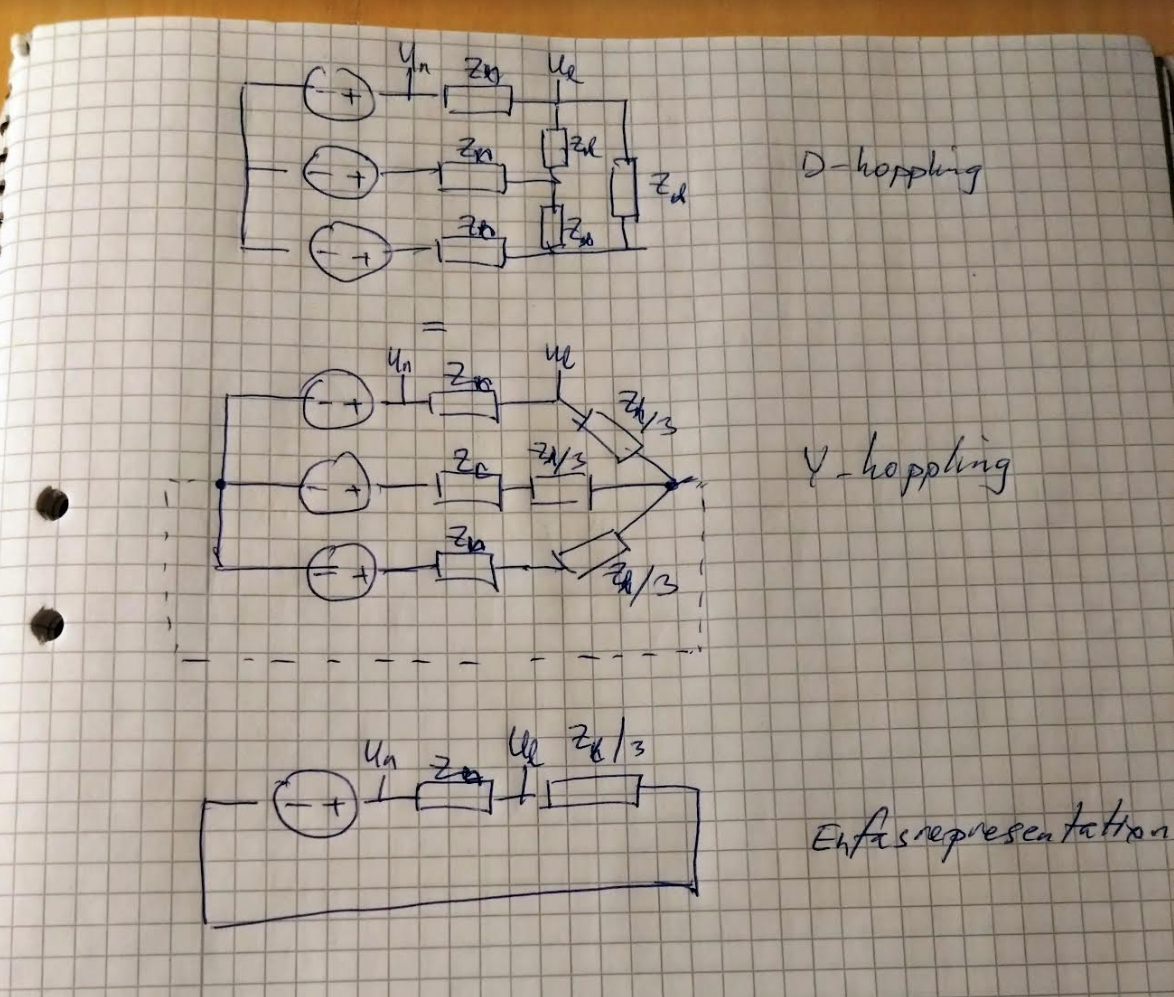
Den belastningen du har är en D-koppling. Man ser det om man ritar om schemat.
Denna D-koppling går att omvandla till en Y-koppling som belastar på samma sätt. När det är symmetrisk belastning så blir 0-punkten 0V.
Då kan man titta på en fas och räkna ut I_h och spänningsdelning.

Leona11, kom du på hur du skulle använda ThomasN's "trefasknep"? (Tack ThomasN! Man får skämmas lite, men det där låg långt bak i huvudet...)

stort tack för hjälpen!