Linalg

Hej!
Har koll på hur man räknar absolut beloppet för u och v men vinkeln mellan dem har jag svårt med. Antar att den krävs iom att vi ej är i ett ON system därav krävs cos x för att räkna ut skalärprodukten.

Vad får du om du multiplicerar ihop u och v rent algebraiskt?

Hur menar du multiplicera u med v? (e1 + 2e2+ 3e3)(2e1-3e2+4e3) ?
Fattar inte hur det ska ta mig vidare

Det är skalärprodukten u*v du ska bestämma. Den är linjär dvs a*(b+c)=a*b+a*c Utnyttja detta i din situation med de två parenteserna som du ska multiplicera ihop. Du får termer av typ te_j*e_koch texten ger dig skalrprodukten av basvektorerna så du behöver inte bestämma några vinklar. Allt går helt algebraiskt till som Laguna föreslår.

$u ∙ v = \sum_{i = 1}^{3} u_{i} e_{i} ∙ \sum_{j = 1}^{3} v_{j} e_{j} = \sum_{i, j} u_{i} v_{j} e_{i} ∙ e_{j} = [\begin{matrix} u_{1} & u_{2} & u_{3} \end{matrix}] [\begin{matrix} e_{1} ∙ e_{1} & e_{1} ∙ e_{2} & e_{1} ∙ e_{3} \\ e_{2} ∙ e_{1} & e_{2} ∙ e_{2} & e_{2} ∙ e_{3} \\ e_{3} ∙ e_{1} & e_{3} ∙ e_{2} & e_{3} ∙ e_{3} \end{matrix}] [\begin{matrix} v_{1} \\ v_{2} \\ v_{3} \end{matrix}]$

Jag fattar fortfarande inte kopplingen mellan multiplikation u och v med skalärprodukt.
Iom ej ON system går det ej att multiplicera fram skalärprodukten? eller fattar jag något fel.

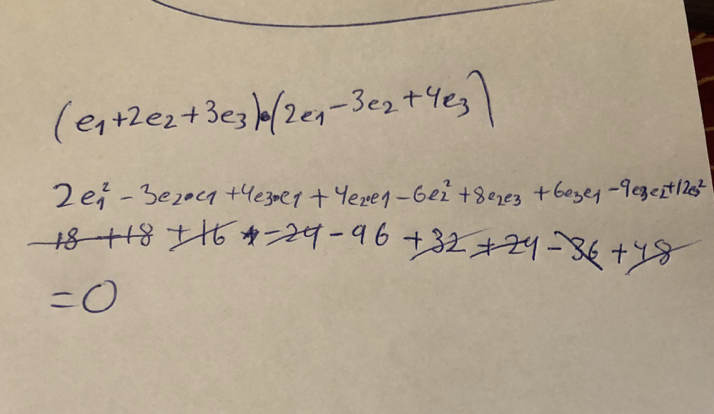Tror möjligtvis jag fått rätt svar men hade inte kunnat motivera det hehe

I ett ON-system behövs inte upplysningarna i texten för då vet man att ej *e_k= 1 om j=k och 0 annars. Skalärprodukter är bilineära. Därför funkar ihopmultipliceringen som jag visat.

Svara

Visa senaste svar