Lin alg. Bestämma planets ekvation
Hej, jag har kämpat en aning med denna uppgift:

Enligt facit kan vektorn PQ ses som en normalvektor till planet, jag förstår inte hur man kan komma till denna slutsats.
Min lösning:
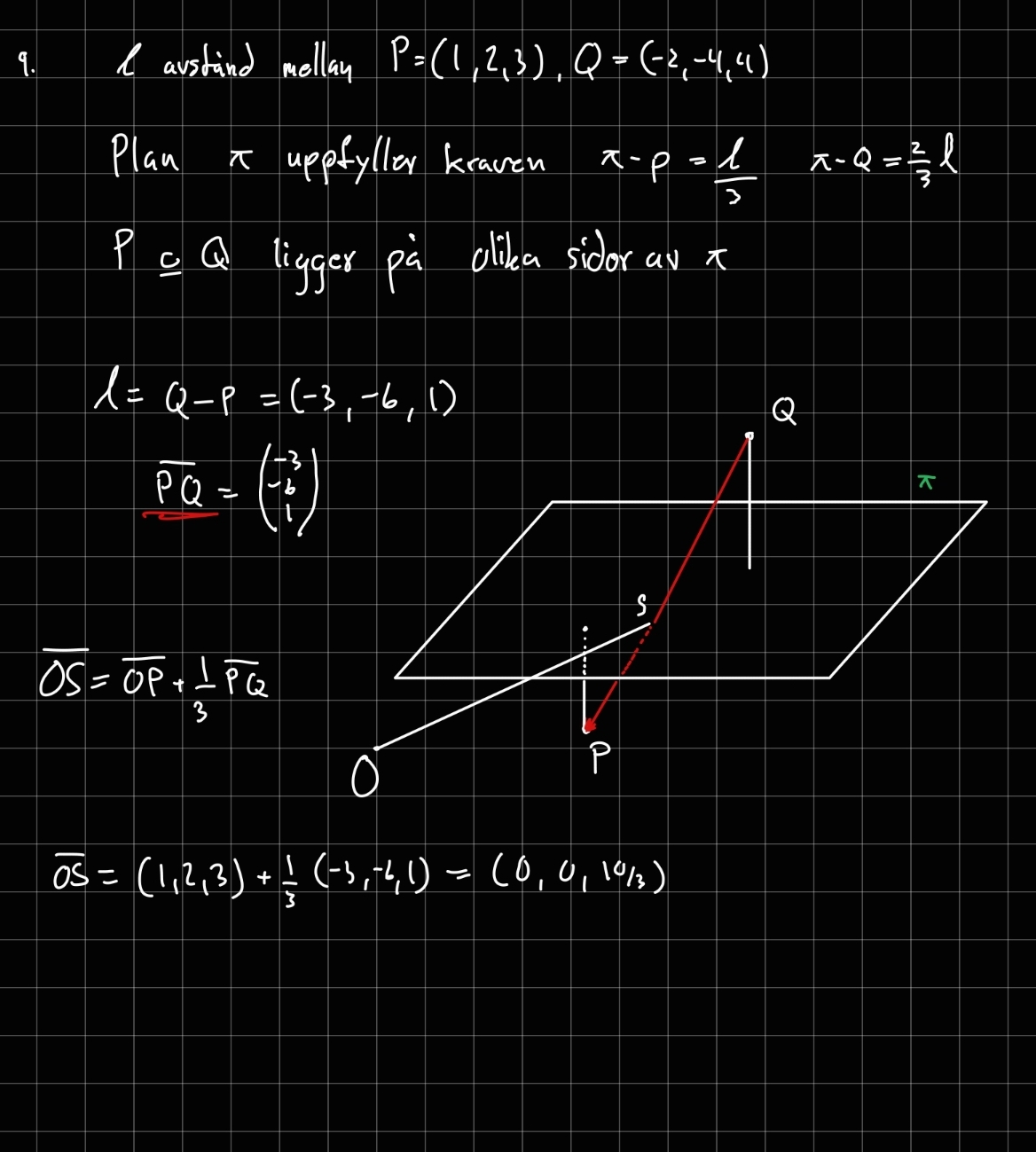
I uppgiften har man bara identifierat en punkt i planet som ligger på vektorn PQ men det finns oändligt antal plan genom den punkten och de kan i övrigt luta åt vilket håll som helst. Nu frågar de efter ekvationen för ETT av dessa plan och då är det enklast att välja det planet som har PQ som normalvektor.
CurtJ skrev:I uppgiften har man bara identifierat en punkt i planet som ligger på vektorn PQ men det finns oändligt antal plan genom den punkten och de kan i övrigt luta åt vilket håll som helst. Nu frågar de efter ekvationen för ETT av dessa plan och då är det enklast att välja det planet som har PQ som normalvektor.
Jag förstår. Om jag förstår dig rätt så kan man orientera planet på vilket sätt som hellst, sålänge kraven för avståndet till Q och P till planet uppfylls. Då kan man skapa ett plan så att vektorn PQ är ortogonal mot planet, dvs är en normal till planet.
Ja så tolkar jag uppgiften och då blir det enklaste att använda den givna vektorn som normal. Någon annan information finns inte i uppgiften.
CurtJ skrev:Ja så tolkar jag uppgiften och då blir det enklaste att använda den givna vektorn som normal. Någon annan information finns inte i uppgiften.
Tack jag begriper det nu!
Jag måste nog be om ursäkt, tänkte inte fullt ut, men avståndet från en punkt till ett plan är ju det vinkelräta avståndet till planet och om det är l/3 från den ena punkten och 2L/3 från den andra så måste vektorn PQ vara normalen.

