Likheter gällande ekvation för p & q

Hej.

På B C och D kan du jobba med potenslagen (a/b)^c = a^c/b^c.

På E kan du göra på olika sätt:

1. Pröva att välja enkla värden på p och q och se om likheten stämmer då. Om nej är svaret klart, om ja så kan du prova andra värden. Om det inte stämmer då så är det klart, men om det stämmer även där bör du fundera på något sätt att visa att likheten stämmer för alla p och q, t.ex. enligt nedan
2. Multiplicera nämnaren I VL med HL, försök att förenkla och se om du då får fram täljaren i VL.

Försökte mig på b. Men i min räkning med potens lagar kommer jag fram till att den är falsk men när jag testat värden stämmer den:(

Maddefoppa skrev:

Försökte mig på b. Men i min räkning med potens lagar kommer jag fram till att den är falsk men när jag testat värden stämmer den:(

Det är nästan omöjligt att läsa vad du skrivit här. Jag ser inte att du någonstans konstaterar att påståendet är falskt (vilket det inte är).

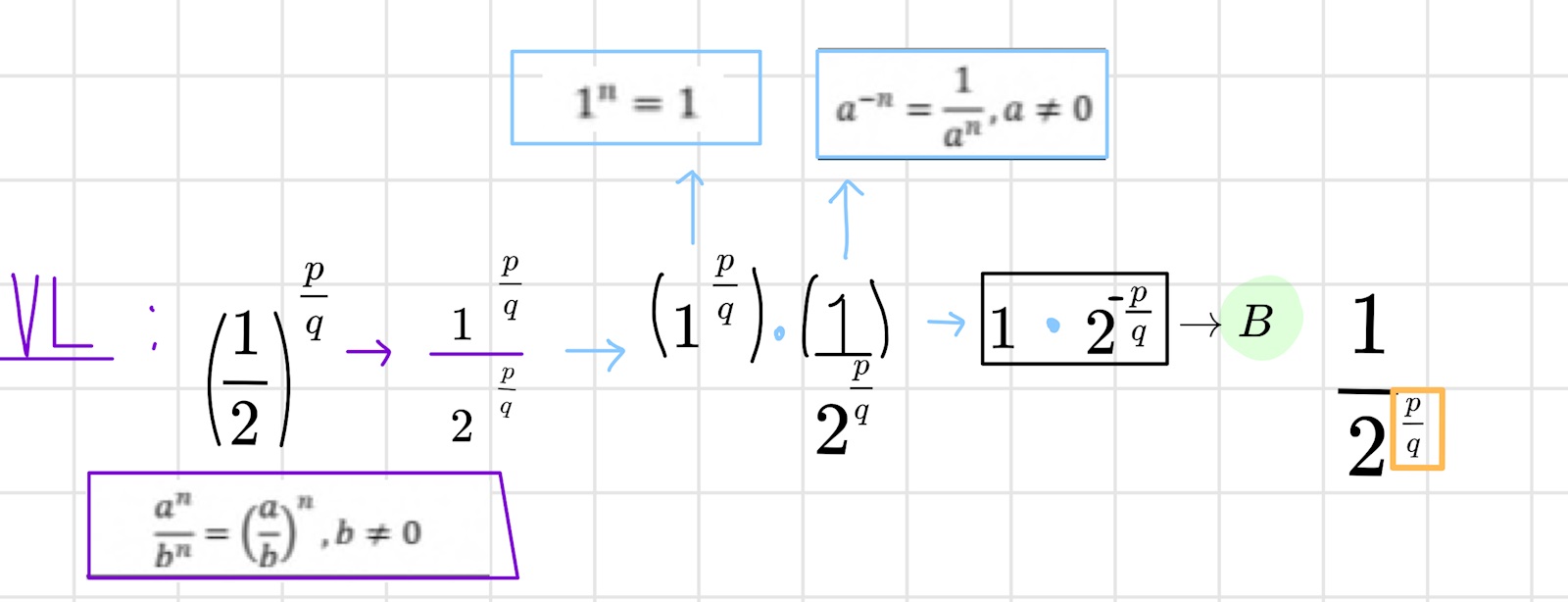
Eftersom exponenten är p/q så ger potenslagen (a/b)ⁿ = aⁿ/bⁿ att (1/2)^p/q = 1^p/q/2^p/q, vilket är samma sak som 1/2^p/q. Var det så du skrev?

ja precis & därmed måste B stämma medans c & d är fel.

syns denna bild ovan bättre?

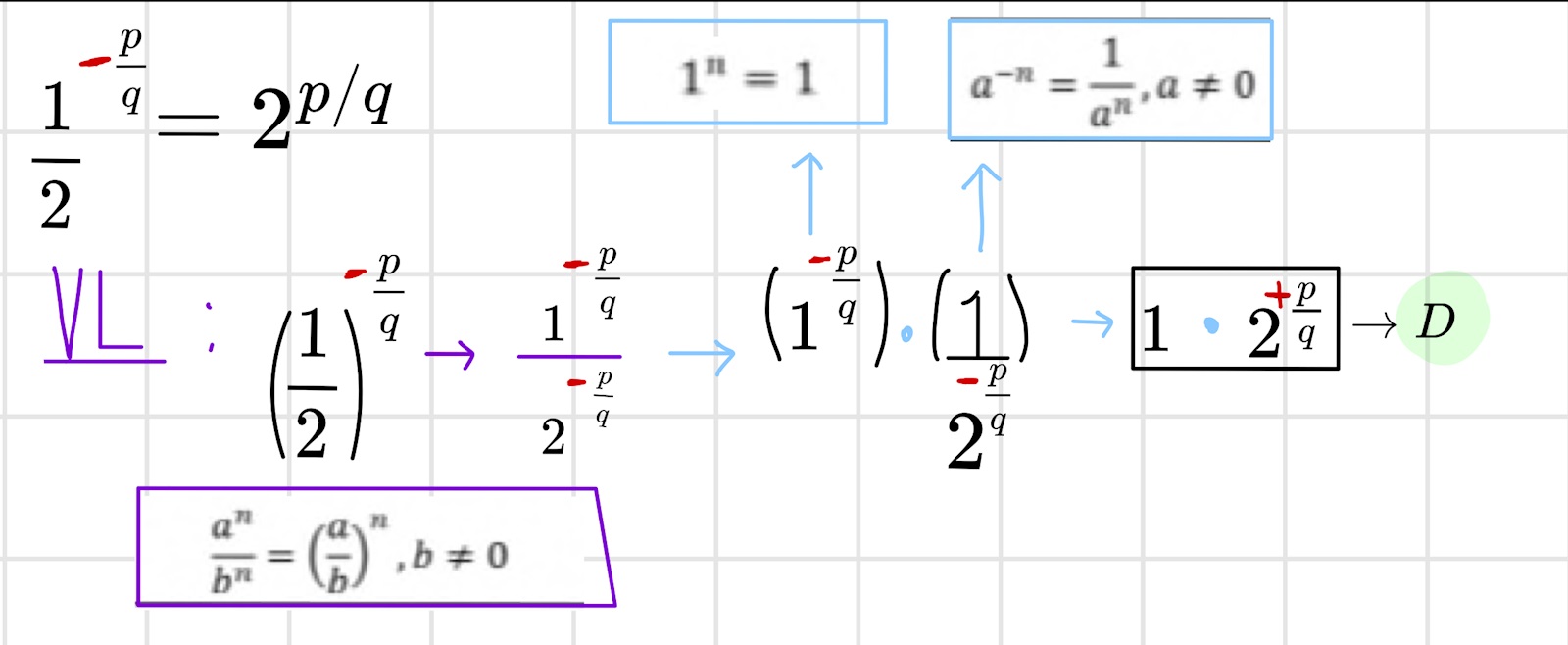
Kom fram till att D inte är fel utan både B & D måste stämma då de enbart har skillda + & minus tecken på VL k& HL. Men däremot A & C är fel. Kan du se dessa bilder bättre?

Testade som du sa på E. med 2 exempel och genereade samma svar. Sen multiplikation. Då blev det konjugat regeln & VL=HL

Ja, nu syns bilderna bättre.

Nej, konjugatregeln lyder x²-y² = (x+y)(x-y).

Den gäller alltså endast då exponenten är lika med 2, vilket inte är fallet här.

A oki så istället bör det blir en variant som liknar konjugat regeln?

Fast med p & q istället för ^2?

Ursprungsekvationen är

$\frac{4^p-4^q}{2^p-2^q}=2^p+2^q$

Vi börjar med att konstatera att det måste gälla att $p\neq q$, annars är vänsterledet odefinierat.

Efter multiplikation med $2^p-2^q$ får vi $4^p-4^q=(2^p-2^q)(2^p+2^q)$

Multiplicera nu ihop högerledet, förenkla och se hur du kan gå vidare därifrån.

HL: ger (2p)2+4p•q-4p•q-(2 ^q)2=

 (2p)²+(2p)²=4^{p^2}+4^{q^2}

Jag är osäker på vad det du skriver betyder.

Det gäller att $(2^p-2^q)(2^p+2^q)=$

$=(2^p)^2+2^p2^q-2^q2^p-(2^q)^2=2^{2p}-2^{2q}$

Kan du fortsätta att skriva om detta uttryck så att exponenterna bara blir p respektive q?