likformighet och topptriangelssatsen

Två trianglar kan vara likformiga utan att den ena är topptriangel i den andra. 
Och likformiga trianglar är ingen sats, det är trianglar. 

Mogens skrev:

Två trianglar kan vara likformiga utan att den ena är topptriangel i den andra. 
Och likformiga trianglar är ingen sats, det är trianglar. 

men för de båda gäller det att vinklarna är lika stora och att sidorna är likformiga. Jag har svårt att se vad skillnaden är-förutom att de har olika namn. 

det topptriangelsatsen egentligen säger är att en triangel och dess topptrianglar alltid är likformiga. så om det är fallet, borde det inte funka på samma sätt-fast tvärtom? att alla likformiga trianglar är topptianglar eftersom de är likformiga och har samma vinklar 

skulle verkligen, verkligen, verkligen uppskatta hjälp så snart som möjligt. Har ett prov imorgon och detta gör mig extremt förvirrad 

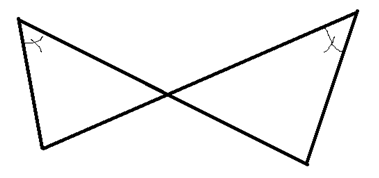
Här är två trianglar som är likformiga men som inte är topptrianglar: (om jag hade ritat mindre snett, alltså...)

Smaragdalena skrev:

Här är två trianglar som är likformiga men som inte är topptrianglar: (om jag hade ritat mindre snett, alltså...)

Om man tar den mindre triangeln och stoppar in i den större så blir det väll en topptriangel? 

Jo det var det jag försökte säga i mitt första inlägg #2

trianglar är likformiga om de har parvis samma vinklar.

om du skär av en triangel med en sida parallell med basen så får du två trianglar med parvis samma vinklar. 
men du kan ha en triangel Blomstermåla och en i Australien. De kan vara likformiga utan att nudda varandra. 

Du bör förstå ordningen här. Först definierar man likformighet. Sedan upptäcker man att fenomenet kan observeras hos topptrianglar.