Likformighet..

Uppgift
A = (1, 1) och B = (−7, 9) är ändpunkterna på sträckan AB.

a) Bestäm koordinaterna för mittpunkten M. Denna var inga problem.

Hur gör jag med denna tycks inte förstå hur jag skall ställa upp den????
b) Punkten K delar sträckan AB i förhållande 2:1 från A räknat. Bestäm koordinaterna för K.

Hur stor är de totala förändringarna i x- och y-led? Dela upp sträckan i tre delar, alla lika stora. Vilka x- och y-koordinater har dessa sträckor?

Smutstvätt skrev:
Hur stor är de totala förändringarna i x- och y-led? Dela upp sträckan i tre delar, alla lika stora. Vilka x- och y-koordinater har dessa sträckor?

Lyckas fortsatt inte ställa upp det korrekt??? :(

Tänker (-7,1) att det skall delas upp på 3...

Avståndet i x-led är $1-(-7)=8$ längdenheter. Alltså måste punkterna ligga $\frac{8}{3}$ längdenheter från varandra i x-led. Kan du göra samma sak för y-ledet?

Smutstvätt skrev:
Avståndet i x-led är $1-(-7)=8$ längdenheter. Alltså måste punkterna ligga $\frac{8}{3}$ längdenheter från varandra i x-led. Kan du göra samma sak för y-ledet?

Hej igen och tack!

Vad är det för formel...?

Då tänker jag att avståndet i y-led blir 1-9=-8

Vidare då x, y = 8/3, -8/3...

Facit säger $b) K = - \frac{13}{3}, \frac{19}{3}$ ?

Har jag ritat rätt?

Många tack

Det gäller eftersom det är en rät linje. Det vi gör är att vi delar upp linjen i tredjedelar:

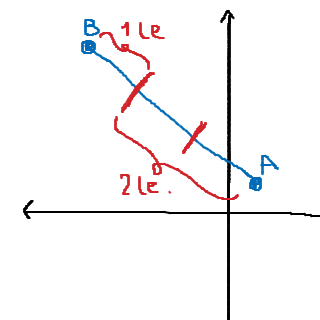(le står för längdenheter)

Sedan kan vi ställa oss i B, och lägga på en av dessa tredjedelssträckor, och då hittar vi punkten som delar sträckan i förhållandet 2:1 till A. :)

Så ja, din beräkning stämmer. För att hitta vår punkt som är 2:1 från A till B, ställer vi oss i B och adderar 1 "x-sträcka" (som är skrivna i tredjedelar) och en "y-sträcka" (också i tredjedelar). Det ger:

$(- 7, 9) + (\frac{8}{3}, - \frac{8}{3}) = (- \frac{13}{3}, \frac{19}{3})$

Vilket stämmer med facit. Jag rekommenderar ändå att du kontrollräknar och ser till att sträckorna uppfyller förhållandekriteriet.

Smutstvätt skrev:
Det gäller eftersom det är en rät linje. Det vi gör är att vi delar upp linjen i tredjedelar:
(le står för längdenheter)
Sedan kan vi ställa oss i B, och lägga på en av dessa tredjedelssträckor, och då hittar vi punkten som delar sträckan i förhållandet 2:1 till A. :)

Så ja, din beräkning stämmer. För att hitta vår punkt som är 2:1 från A till B, ställer vi oss i B och adderar 1 "x-sträcka" (som är skrivna i tredjedelar) och en "y-sträcka" (också i tredjedelar). Det ger:
$(- 7, 9) + (\frac{8}{3}, - \frac{8}{3}) = (- \frac{13}{3}, \frac{19}{3})$
Vilket stämmer med facit. Jag rekommenderar ändå att du kontrollräknar och ser till att sträckorna uppfyller förhållandekriteriet.

Aaah! Punkt B:s x och y-koordinat + förändringen i x och y-led.

$\frac{8}{3} = 2, 666 . . r e s p . - \frac{8}{3} = - 2, 666 . . (- 7 + 2, 666 . . . = - 4.333 . . . s o m ä r s a m m a s a k s o m - 7 + \frac{8}{3} . .) S t ä m m e r ä v e n i y - l e d$

:-D Tack snäll du!

Precis så! Bra jobbat!

Smutstvätt skrev:
Precis så! Bra jobbat!

Va nu da....:(

Skulle göra nästa c) Punkten N delar sträckan AB i förhållande 3:2 från A räknat. Bestäm koordinaterna för N.

Tänker då att det är samma som ovan fast 5 istället för 3???

Men det stämde inte :( fick det till;

$(- 7, 9) + \frac{8}{5}, - \frac{8}{5} = - 7 + \frac{8}{5}, 9 + (- \frac{8}{5}) = - \frac{27}{5}, \frac{37}{5}$

Facit säger $- \frac{19}{5}, \frac{29}{5}$ ???

Du har räknat med att punkten är 1/5 från B, inte 2/5.

x-koordinat: $-7+\frac{2}{5}\cdot8=-\frac{-35+16}{5}=-\frac{19}{5}$

Kan du ta fram y-koordinaten själv?

Smaragdalena skrev:
Du har räknat med att punkten är 1/5 från B, inte 2/5.
x-koordinat: $-7+\frac{2}{5}\cdot8=-\frac{-35+16}{5}=-\frac{19}{5}$
Kan du ta fram y-koordinaten själv?

Tänker då att jag skall ta $9 + (\frac{3}{5}) \times - 8 m e n d e t b l i r \frac{21}{5} . . .$

Hmm, suck.. behöver hjälp även med y dessvärre..

Om avståndet mellan A och P är 3/5 av avståndet mellan A och B, så är avståndet mellan P och B 2/5 av avståndet mellan A och B. Antingen räknar du med punkten A och 3/5, eller med punkten B och 2/5. När du blandar ihop de båda, räknar du ut y-koordinaten för fel punkt.

Smaragdalena skrev:
Om avståndet mellan A och P är 3/5 av avståndet mellan A och B, så är avståndet mellan P och B 2/5 av avståndet mellan A och B. Antingen räknar du med punkten A och 3/5, eller med punkten B och 2/5. När du blandar ihop de båda, räknar du ut y-koordinaten för fel punkt.

Ok då fattar jag..

räknar alltså även y med 2/5 då jag ju utgår från punkten B i detta fall och nu stämmer det! :)

Tack för detta!

Svara Avbryt

Visa senaste svar