Längd mellan två hörn i en regelbunden femhörning

Om detta är en regelbunden femhörning där varje sida är 5 cm, då antar jag att man kan räkna ut hur lång sträckan AD är. Hur gör man det?

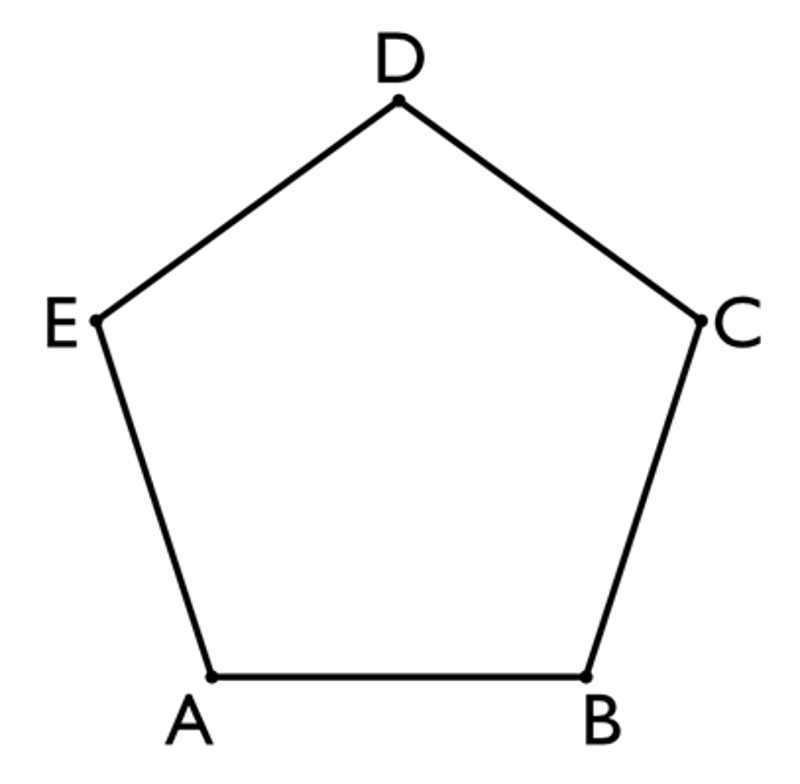
Då blir AED en likbent triangel. Där vinkeln vid E är känd som 3*180/5 = 108 grader.

AED är då en likbent triangel så de två okända vinklarna är identiska, (180-108)/2 = 36 grader.

Denna triangel kan man då dela in i två rätvinkliga trianglar genom att dra en linje från den skapta AD-linjen till E.

Sedan är det triogometriska formler som används, med kända hypotenusor och kända vinklar.

Bedinsis skrev:
Sedan är det triogometriska formler som används, med kända hypotenusor och kända vinklar.

Gött! Vilka trigonometriska formler använder man här då?

Cosinusfunktionens definition för att få ut vad halva sträckan AD blir.

Svara Avbryt