kvadratkomplettera -3x^2+2x+8

Du glömmer faktorn -1 och ett x efter 2/3

Hälften av två tredjedelar är helt enkelt lika med en tredjedel.

Yngve skrev:

Du glömmer faktorn -1 och ett x efter 2/3

Hälften av två tredjedelar är helt enkelt lika med en tredjedel.

jag får det till x=$\sqrt{\frac{10}{3}}+\frac{1}{3}$

hur fortsätter jag

Vad menar du med att x har det värdet?

Det är ingen ekvation du ska lösa och du ska inte beräkna något värde på x.

Du ska skriva om det givna uttrycket med hjälp av kvadratkomplettering, dvs du ska skriva uttrycket på formen $(x+a)^2+b$.

Om du berättar hur du tänker och visar dina uträkningar så är det enklare för oss att hjälpa dig.

Yngve skrev:

Vad menar du med att x har det värdet?

Det är ingen ekvation du ska lösa och du ska inte beräkna något värde på x.

Du ska skriva om det givna uttrycket med hjälp av kvadratkomplettering, dvs du ska skriva uttrycket på formen $(x+a)^2+b$.

Om du berättar hur du tänker och visar dina uträkningar så är det enklare för oss att hjälpa dig.

jag fick x till +-6/3

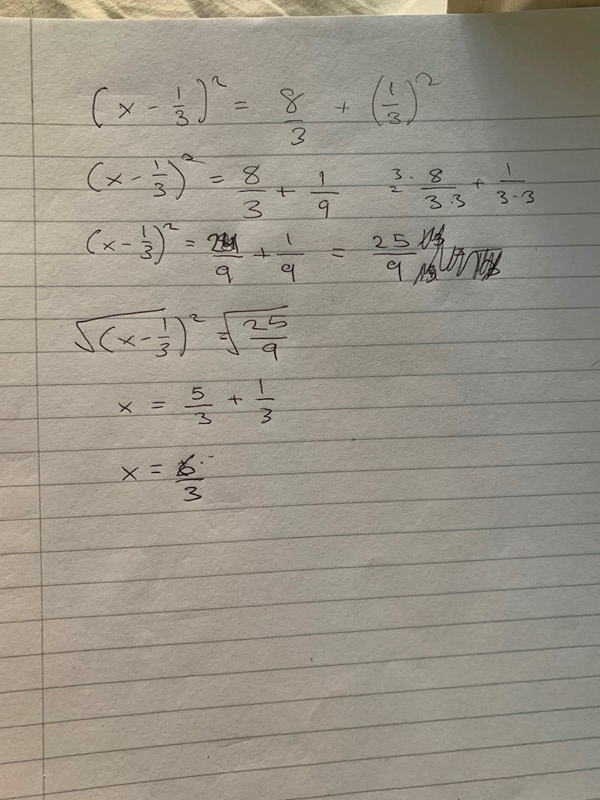
Hir lyder uppgiften?

Ska du lösa en ekvation eller ska du kvadratkompletteta uttrycket?

Yngve skrev:

Hir lyder uppgiften?

Ska du lösa en ekvation eller ska du kvadratkompletteta uttrycket?

det står kvadratkomplettera har jag räknat för långt kanske

Yngve skrev:

Hir lyder uppgiften?

Ska du lösa en ekvation eller ska du kvadratkompletteta uttrycket?

det blir -3((x-1/3)^2-25/9) sen på b står det

Vilket är det lägsta
värdet uttrycket kan anta och för vilket/vilka värden på x antas detta värde? (Det är inte meningen att du ska använda derivator, utan svaret ska läsas ut ur uträkningen på (a).)

Du har löst ekvationen -3x³+2x+8 = 0.

Men det du skulle göra var att skriva om uttrycket på kvadratkompletterad form.

mattegeni1 skrev:

det blir -3((x-1/3)^2-25/9)

OK bra, har du kontrollerat att det stämmer?

sen på b står det

Vilket är det lägsta
värdet uttrycket kan anta och för vilket/vilka värden på x antas detta värde? (Det är inte meningen att du ska använda derivator, utan svaret ska läsas ut ur uträkningen på (a).)

Och vet du hur du ska kunna ta reda på detta?

Yngve skrev:

mattegeni1 skrev:

det blir -3((x-1/3)^2-25/9)

OK bra, har du kontrollerat att det stämmer?

sen på b står det

Vilket är det lägsta
värdet uttrycket kan anta och för vilket/vilka värden på x antas detta värde? (Det är inte meningen att du ska använda derivator, utan svaret ska läsas ut ur uträkningen på (a).)

Och vet du hur du ska kunna ta reda på detta?

nej det vet jag inte hur gör jag sen?

Har du kontrollerat att din kvadratkomplettering stämmer?

Och frågar de verkligen efter lägsta värdet i uppgiften?

Det är nog bäst att du lägger upp en bild av hela uppgiften.

Yngve skrev:

Har du kontrollerat att din kvadratkomplettering stämmer?

Och frågar de verkligen efter lägsta värdet i uppgiften?

Det är nog bäst att du lägger upp en bild av hela uppgiften.

OK då står det nog bara fel i b-uppgiften. 

Extrauppgift till dig: Varför tror jag det?

Yngve skrev:

OK då står det nog bara fel i b-uppgiften. 

Extrauppgift till dig: Varför tror jag det?

jag föstår inte vad dom vill i b vill dom att jag hittar vad x= är ?

Det står att du ska hitta det lägsta värdet som uttrycket kan anta.

(Och att du även ska ange vilket/vilka värden på x som ger detta minsta värde.)

Förtydligande:

Om vi kallar uttrycket för f(x), dvs f(x) = -3x²+2x+8, så vill de att du ska ange det lägsta värdet som f(x) kan anta.

(Och vilket/vilka värden på x som ger detta lägsta värde.)

Du vet väl vad ett lägsta värde är?

Yngve skrev:

Det står att du ska hitta det lägsta värdet som uttrycket kan anta.

(Och att du även ska ange vilket/vilka värden på x som ger detta minsta värde.)

Förtydligande:

Om vi kallar uttrycket för f(x), dvs f(x) = -3x²+2x+8, så vill de att du ska ange det lägsta värdet som f(x) kan anta.

(Och vilket/vilka värden på x som ger detta lägsta värde.)

Du vet väl vad ett lägsta värde är?

menar dom att jag ska ta reda på vad x blir? jag förstår inte riktig hur man annars ska fortsätta räkna

De vill att du ska reda på vad x blir då uttrycket antar sitt lägsta värde. Och de vill även att du ska ange detta lägsta värde.

===========

Exempel: Uttrycket x²+1 har ett lägsta värde. Detta lägsta värde är 1. Det lägsta värdet antas då x = 0. Minimipunkten är (0, 1). Rita grafen till y = x²+1 så ser du vad jag menar.

Förstår du då vad ett lägsta värde är?

Yngve skrev:

De vill att du ska reda på vad x blir då uttrycket antar sitt lägsta värde. Och de vill även att du ska ange detta lägsta värde.

===========

Exempel: Uttrycket x²+1 har ett lägsta värde. Detta lägsta värde är 1. Det lägsta värdet antas då x = 0. Minimipunkten är (0, 1). Rita grafen till y = x²+1 så ser du vad jag menar.

Förstår du då vad ett lägsta värde är?

jag tror dom menar högsta värdet eftersom det står minustecken framför x^2

Ja det tror jag med.

Då kan vi gå vidare med uppgiften.

Har du kontrollerat att ditt förslag på kvadratkomplettering är korrekt?

Yngve skrev:

Ja det tror jag med.

Då kan vi gå vidare med uppgiften.

Har du kontrollerat att ditt förslag på kvadratkomplettering är korrekt?

nej hur kontrollerar man? men jag har räknat på 2 sätt både med att bryta ut -3 och med att dividera med 3 och fått samma svar så tror inte det är fel

På samma sätt som du kontrollerar att en faktorisering är korrekt:

Multiplicera ihop ditt kvadratkompletterade uttryck igen. Får du då tillbaka ursprungsuttrycket så är chansen stor att kvadratkompletteringen var korrekt.

Detta bör du alltid göra för att hitta eventuella fel på ett tidigt stadium och därmed minska risken för en massa onödigt arbete.

Yngve skrev:

På samma sätt som du kontrollerar att en faktorisering är korrekt:

Multiplicera ihop ditt kvadratkompletterade uttryck igen. Får du då tillbaka ursprungsuttrycket så är chansen stor att kvadratkompletteringen var korrekt.

Detta bör du alltid göra för att hitta eventuella fel på ett tidigt stadium och därmed minska risken för en massa onödigt arbete.

nu är jag på e) jag har fått -(x-2)(3x+4) tidigare är svaret på e) (x-2)  x$\not\equiv$2 och (3x+4) x$\not\equiv$ vet jag inte?

Nej läs frågan ordentligt. Vad är det de frågar efter egentligen?

Yngve skrev:

Nej läs frågan ordentligt. Vad är det de frågar efter egentligen?

det står ju för vilka värden för x blir uttrycket är 0?

Ja. Frågan gäller alltså vilka värden på x som gör att uttrycket -(x-2)(3x+4) har värdet 0.

Det vill säga du ska leta efter lösningarna till ekvationen -(x-2)(3x+4) = 0

I vänsterledet står en produkt mellan två faktorer. Denna produkt ska ha värdet noll.

Kommer du vidare då?

Yngve skrev:

Ja. Frågan gäller alltså vilka värden på x som gör att uttrycket -(x-2)(3x+4) har värdet 0.

Det vill säga du ska leta efter lösningarna till ekvationen -(x-2)(3x+4) = 0

I vänsterledet står en produkt mellan två faktorer. Denna produkt ska ha värdet noll.

Kommer du vidare då?

(x-2) blir 0 när x=2
(3x+4) blir 0 när x= -4/3 


stämmer det?

mattegeni1 skrev:

stämmer det?

Pröva!

Yngve skrev:

mattegeni1 skrev:

stämmer det?

Pröva!

en fråga vad betyder -3x^2 jag vet att minustecken betyder maximum men vad betyder 3an

Koefficienten framför x²-termen bestämmer hur kraftigt "skålad" motsvarande parabel är.

Ju större värde på koefficienten, desto "brantare" parabel.

Sedan har koefficienten även betydelse för maxpunktens placering, både i x- och y-led.

Pröva gärna lite olika värden med hjälp av Desmos eller något annat digitalt grafritande hjälpmedel.

Yngve skrev:

Koefficienten framför x²-termen bestämmer hur kraftigt "skålad" motsvarande parabel är.

Ju större värde på koefficienten, desto "brantare" parabel.

Sedan har koefficienten även betydelse för maxpunktens placering, både i x- och y-led.

Pröva gärna lite olika värden med hjälp av Desmos eller något annat digitalt grafritande hjälpmedel.

ja jag har provat och jag ser att nollpunkterna ändras beroende på koefficienten framför x^2 ? sen undrar jag vad 2x betyder det betyder väl att för varje ruta så skär den 2 rutor? men i demos skär den 4-5 rutor enligt uttrycket?

mattegeni1 skrev:

ja jag har provat och jag ser att nollpunkterna ändras beroende på koefficienten framför x^2 ?

Ja, allt ändras. Nollställen, maxpunktens placering och parabelns "branthet".

sen undrar jag vad 2x betyder det betyder väl att för varje ruta så skär den 2 rutor? men i demos skär den 4-5 rutor enligt uttrycket?

Nej du blandar ihop det med linjära funktioner, dvs y = kx + m, där k anger linjens lutning, dvs desd riktningskoefficient.

För ett andragradsuttryck påverkar faktorn framför förstagradstermen var min/maxpunkten hamnar i x-led. Pröva dig fram även här.