Kurvintegral, Greens formel
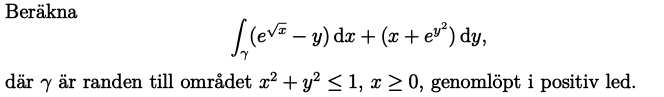
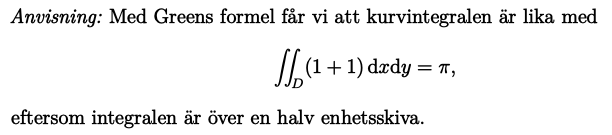
Förstår inte riktigt varför man inte drar bort kurvintegralen då y=0? Tänker alltså eftersom vi använder greens formel så måste ju kurvan vara sluten, vilket inte en halv cirkelskiva är, men vi kan ju sluta den genom att lägga till linjen y=0. Men då brukar man ju alltid räkna ut kurvintegralen för denna också för att sedan dra bort. Varför gör man inte det i detta fall?
Man tänker sig att "randen till området" innesluter hela det specificerade området, dvs kurvan inkluderar den bit du pratar om att dra bort. Med andra ord är det en sluten kurvintegral. Cirkelskivan är sluten.
Normalt sett gäller att när man pratar om randen till ett område menar man den begränsning som "innesluter" området. Randen är en dimension lägre än området. T.ex. är randen till ett område i två dimensioner en sluten kurva. Randen till en volym i 3 dimensioner är en sluten yta osv.
Jag tror också att du slarvar till området. Linjen som sluter halvcirkeln är x=0, y=1 till y=-1, inte y=0.
D4NIEL skrev:Man tänker sig att "randen till området" innesluter hela det specificerade området, dvs kurvan inkluderar den bit du pratar om att dra bort. Med andra ord är det en sluten kurvintegral. Cirkelskivan är sluten.
Normalt sett gäller att när man pratar om randen till ett område menar man den begränsning som "innesluter" området. Randen är en dimension lägre än området. T.ex. är randen till ett område i två dimensioner en sluten kurva. Randen till en volym i 3 dimensioner är en sluten yta osv.
Jag tror också att du slarvar till området. Linjen som sluter halvcirkeln är x=0, y=1 till y=-1, inte y=0.
oj, menar menar självklart att man skulle lägga till x=0. men förstår inte helt hur du menar ändå, hur kan x=0 ingå där när man bar beskriver randen till cirkeln, borde inte den halva cirkelskivan "vara öppen" åt vänster i så fall?
Jag förstår hur du menar, men om du tittar på uppgiften säger de inget om en cirkel, de specificerar bara ett område enligt .
Det innebär område C i figuren nedan, och randen till området är den röda linjen som går runt hela område C. Du hade förmodligen accepterat randkurvan som innesluter A utan problem, liksom B. Det är egentligen ingen skillnad, randen till området ska innesluta området.

Tillägg: 22 okt 2023 14:59
Rättelse:
D4NIEL skrev:Jag förstår hur du menar, men om du tittar på uppgiften säger de inget om en cirkel, de specificerar bara ett område enligt .
Det innebär område C i figuren nedan, och randen till området är den röda linjen som går runt hela område C. Du hade förmodligen accepterat randkurvan som innesluter A utan problem, liksom B. Det är egentligen ingen skillnad, randen till området ska innesluta området.
hmm okej, men i denna videon (https://www.youtube.com/watch?v=VETtS88dgT8&list=PL2w8yt28pgXpNK0sgQQ8nqae3-No9Y_Mw&index=103) så är det ju samma område, men där drar han bort den linjen han lagt till för att skapa ett slutet område? alltså x=0.
I den uppgiften anges explicit att man ska beräkna kurvintegralen från (0,-1) till (0,1) under villkoret . Det innebär den röda delen av kurvan nedan:

Notera också att är en kurva (1 dimension) medan är ett område (2 dimensioner). Randkurvan till området är sluten. Därför måste man dra bort den svarta delen om man räknar med Greens formel och bara är intresserad av den röda kurvan.
I den ursprungliga uppgiften var de intresserade av integralen längs hela randkurvan runt området, dvs röd + svart del. Är du med?

