Kulans hastighet
En liten kula är fäst i en 1,2 m lång tråd. Man låter kulan utföra en konisk pendelrörelse så att tråden bildar vinkeln 35⁰ med lodlinjen. Bestäm kulans hastighet.
Kan någon vägleda mig?
Kan du skapa och ladda upp en skiss med krafterna som utövas på kulan?
Macilaci skrev:Kan du skapa och ladda upp en skiss med krafterna som utövas på kulan?
Jag kan inte riktigt se scenariot framför mig.
Vet inte hur jag ska göra skissen där en kula "utför en konisk pendelrörelse så att tråden bildar vinkeln 35⁰ med lodlinjen"
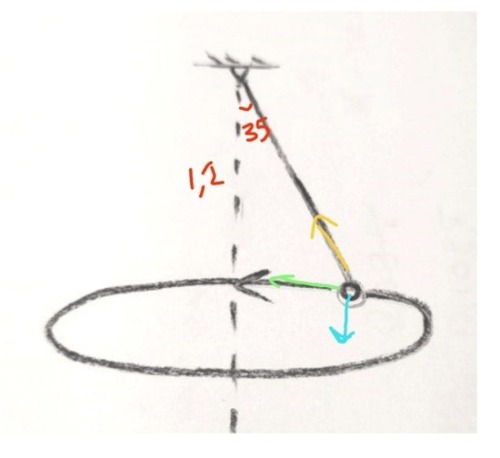
Kulan snurrar runt så här:

Skissen jag menade:

Snyggt, hur såg du detta? Det makear sense nu i efterhand men hade inte kommit på det där.
Jag lade till detta
Tillägg: 24 sep 2023 22:27
Gul är spännkraft.
Grön centripetalkraft.
Blå tyngdkraft.
Bra!
(OBS 1,2m är längden på snöret.)
Centripetalkraften kan du beräkna med hjälp av radien.
Fres = Fcp
Fres måste vara horisontell eftersom kulan accelererar bara horisontellt.
Fres kan du beräkna med hjälp av vinkeln och tyngdkraften.
Hastigheten kan du beräkna med hjälp av centripetalkraften och radien.
Macilaci skrev:Bra!
(OBS 1,2m är längden på snöret.)
Oj, ja
Centripetalkraften kan du beräkna med hjälp av radien.
Fres = Fcp
Varför och hur vet man detta? Är det eftersom det är den kraften vi ser när man snurrar? Kan man ha som tumregel att Fres alltid är Fcp vid cirkelbanor? (Om den är större än centrifugalkraften?)
Fres måste vara horisontell eftersom kulan accelererar bara horisontellt.
Ja
Fres kan du beräkna med hjälp av vinkeln och tyngdkraften.
Alltså den horisontella kraften? Jag har längden på snöret 1,2m och radien är den vi söker efter:
Sin(35) = r/1,2 ≈ 0,69 m.
Hastigheten kan du beräkna med hjälp av centripetalkraften och radien.
Hur? Vi har väl inte centripetalkraften?
Kan man ha som tumregel att Fres alltid är Fcp vid cirkelbanor? (Om den är större än centrifugalkraften?)
Ja, om vi har en likformig cirkelrörelse (dvs konstant hastighet). Om Fres är större än centripetalkraften, lämnar kulan cirkelbanan (utåt).
-----------
För att beräkna Fres behöver du inte radien. Fres = mg*tg(35o)
(Se min skiss i #5)
-----------
Hastigheten kan du beräkna med hjälp av centripetalkraften och radien.
Hur? Vi har väl inte centripetalkraften?
Jo, vi har den. Fcp = Fres vilken du har just beräknat (se ovan).
Ah, snyggt. Tack!
Tillägg: 24 sep 2023 23:05
Förresten hur fås centripetalkraften ut genom tyngdkraften? Hur är de "beroende" av varandra?
Kan man "alltid" göra så med centripetalkraften? (Få den genom tyngdkraften?) Hur funkar det? (Matematiskt förstår jag det men inte ur ett "fysiskt" håll)
Du kan resonera så här (tänk på skissen i #5) :
1) Vi beräknar Fs först. Dess vertikala komposant måste vara lika med mg (eftersom kulan inte accelererar vertikalt).
Fsy = mg
Fs = Fsy / cos(35o)
2) Vi beräknar Fsx som blir den resulterande kraften eftersom Fs är den enda kraft som har horisontell komposant.
Fsx = Fs * sin(35o) = Fsy*tan(35o) = mg*tan(35o)
Tack så mycket för svaret, men jag var mer ute efter hur man kan få fram centripetalkraft utifrån mg. Jag förstår att det fås genom trigonometri. Men hur hör de ihop och gör att man kan få centripetalkraften ur mg?
Jag tror inte att det finns något "recept" för att få Fcp ur mg. Det beror på situationen. Det är därför väldigt viktigt att rita en exakt skiss av alla krafter. Som sagt, oftast är centripetalkraften den resulterande kraften. (Om rörelsen är en likformig cirkulär rörelse.)
Macilaci skrev:Jag tror inte att det finns något "recept" för att få Fcp ur mg. Det beror på situationen. Det är därför väldigt viktigt att rita en exakt skiss av alla krafter. Som sagt, oftast är centripetalkraften den resulterande kraften. (Om rörelsen är en likformig cirkulär rörelse.)
Visst bör egentligen mg vara större än Fres (centripetalkraften)?
Jag har läst att ett föremål nödvändigtvis inte rör sig åt det håll där den resulterande kraften är riktad, utan istället åt det håll hastigheten är riktad. Är det så i detta fallet? Och hur fungerar detta egentligen?
Visst bör egentligen mg vara större än Fres (centripetalkraften)?
Tyvärr, inte. Ta våran uppgift med en vinkel större än 45o. Fres blir större än mg.
Den kan faktiskt bli mycket större än mg.
Macilaci skrev:Visst bör egentligen mg vara större än Fres (centripetalkraften)?
Tyvärr, inte. Ta våran uppgift med en vinkel större än 45o. Fres blir större än mg.
Den kan faktiskt bli mycket större än mg.
Jaha okej, juste,. Jag tänkte bara på själva kompusantuppdelningen (fg×tan(35)) som Fres , men kom på nu att centripetalkraften fås genom formeln mv2/r, och inte enbart från trigonometrin.
Men hur fungerar det annars? (Det med att Fres inte nödvändigtvis inte är den största kraften, utan att det är hastighetens riktning som "dominerar"?
Tillägg: 25 sep 2023 11:49
Eller vänta i detta fallet fås ju centripetalkraften från enbart (mg×tan(35)?
Det med att Fres inte nödvändigtvis inte är den största kraften...
Det förstår jag inte. Fres är ju inte en av krafterna utan summan av alla krafter.
Man ska tänka på centripetalkraften som kraften som behövs för att tyngden ska röra sig på en cirkelbana. Om den resulterande kraften är lika med den, har vi en likformig cirkulär rörelse.
i detta fallet fås ju centripetalkraften från enbart (mg×tan(35)?
Ja och nej. Det är både mg och dragkraften som samverkar så att Fres blir horisontell.
mg×tan(35) är inte en kraft i sig. Det är storleken på Fres.
Jag syftade på detta "påstående":


