Kritiska punkter R3->R

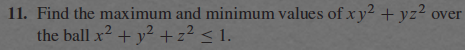
Inre punkter:

$f \left( x,y,z \right)=xy^2+yz^2$

$\nabla \left( x,y,z \right)=\left( y^2, 2xy+z^2, 2yz \right)=0$

$y^2=0$

$2xy+z^2=0$

$2yz=0$

Hur ser jag här att alla värden för x är kritiska punkter?

Ekvationen $y^2=0$ ger att $y\equiv 0$

Sätter vi in det värdet i den andra ekvationen får vi $2x\cdot 0+z^2=0 \implies z^2=0$ och alltså är $z\equiv 0$

Den tredje ekvationen är alltid uppfylld givet att $y=0$ eller $z=0$ . Kan du hitta något värde på $x$ för vilken någon av ekvationerna är falska, givet att $z=y=0$ ?

D4NIEL skrev:
Ekvationen $y^2=0$ ger att $y\equiv 0$

Sätter vi in det värdet i den andra ekvationen får vi $2x\cdot 0+z^2=0 \implies z^2=0$ och alltså är $z\equiv 0$

Den tredje ekvationen är alltid uppfylld givet att $y=0$ eller $z=0$ . Kan du hitta något värde på $x$ för vilken någon av ekvationerna är falska, givet att $z=y=0$ ?

Nej det kan jag inte. Tack :)

Svara