Kritiska punkter flervar

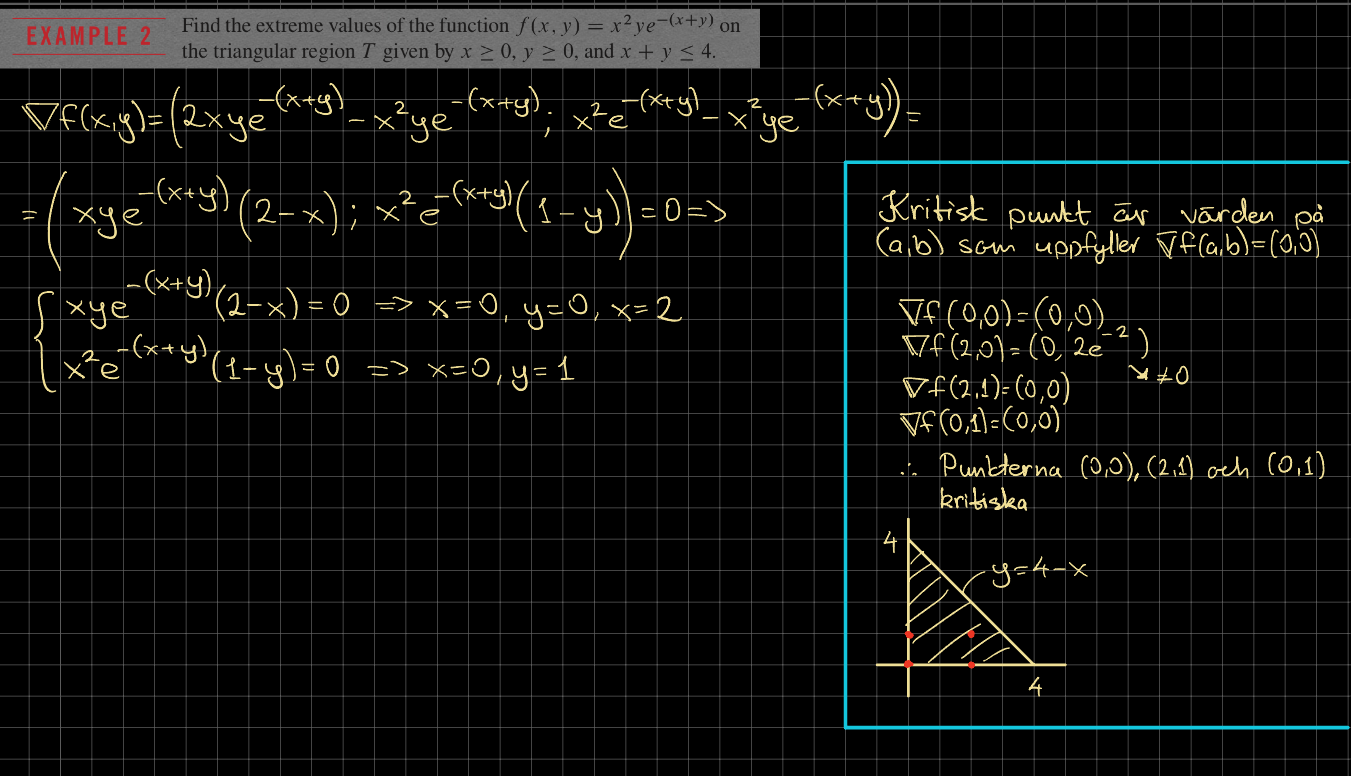
Om x=0 så är f_x =0 för alla y. Därav beteckningen (0,y), men sedan har vi ju ytterligare villkor som ska uppfyllas och dom ger närmare bestämning av y.

Tomten skrev:

men sedan har vi ju ytterligare villkor som ska uppfyllas och dom ger närmare bestämning av y.

Du tänker på begränsningarna av regionen T? Så (0,0) och (0,1) är inte nödvändigtvis fel

Har vi inte också att en kritisk punkt är (2,y)? för om x=2 i f_x så spelar det ingen roll vad y är, högerledet blir ju ändå 0.

Svaret måste bli Ja på båda frågorna. Sedan återstår den tredje sidan och alla inre punkter, men det verkar väl utrett i texten du givit oss.

Tomten skrev:

Svaret måste bli Ja på båda frågorna. Sedan återstår den tredje sidan och alla inre punkter, men det verkar väl utrett i texten du givit oss.

Jag har lite svårt att förstå varför de väljer att uttrycka den kritiska punkten som (2,1) och inte (2,y)?

Vilken är den partiella derivatan i y-led i punkten (2,y)?

Smaragdalena skrev:

Vilken är den partiella derivatan i y-led i punkten (2,y)?

y=1

Tillägg: 9 mar 2023 14:17

Jag tror jag är med

Om jag förstår rätt av texten så är $\left( \frac{8}{3} , \frac{4}{3} \right)=0.17$ inte en extrempunkt av f då $\left( \frac{8}{3} , \frac{4}{3} \right)$ inte är en kritisk punkt till f, utan till g.