Kretsanalys 4.15 - Maskanalys

Hej!

Kan du visa ett uträkningsförsök? Då är det lättare att prata kring uppgiften, se var du tänker fel, och hur du ska tänka istället.

Det man ofta har problem med är hur man ska behandla strömkällan? Är det så?

Först räknar jag KVL på ia till:

-8 - 20ia - 60(ia-ib) = 0

Sedan räknar jag ib och ic som en supermesh:

-60(ia-ib) - 10 - 30ic - 18 = 0

Sätter sedan:

ic = ib + 0.3

Med detta borde jag kunna lösa ut ekvationerna, men får ej i närheten rätt svar

Det ser ut som att du har gjort ett teckenfel på det du kallar "supermesh" (vad är det?)

-60(ia-ib) - 10 - 30ic - 18 = 0

Jag kallar det KVL på nedanstående loop:

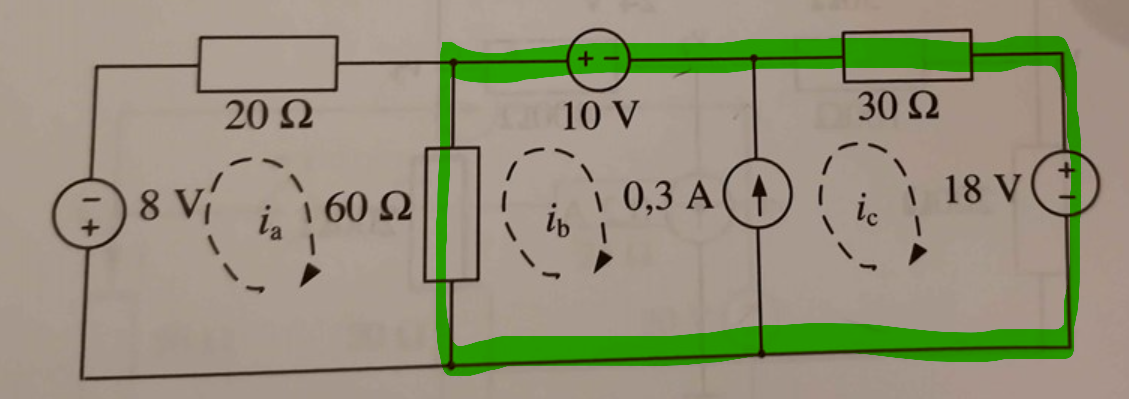
och får det till (medsols från nedre noden):

60(ia-ib) - 10 - 30ic - 18 = 0

Tänker du på något annat sätt?

Enligt min bok kallas looparna mask eller mesh på engelska.

När man gör en mask som sammansätter flera maskor kallas det supermask/supermesh 

Ok men då var jag förhoppningsvis inte helt fel ute. Men jag tror jag testat med även detta och får ej rätt svar när jag löser ekvationssystemet 

Du är absolut inte helt fel ute, och vi är uppenbarligen inne på samma tänk. Vad ska rätt svar vara enligt facit? (facit kan ha fel ibland också...) 

Jag har sett supermesh nämnas tidigare, men man kan också lösa det här problemet "på riktigt", med maskanalys. Då ska man enligt algoritmen först transformera alla strömkällor till spänningskällor:

Detta ger oss det totala nätet

Nu vill vi lösa ekvationssystemet $R_{ij}\mathbf{i}=\mathbf{v}$ där  $R_{ii}$ summa resistanser maska $i$, $-R_{ij}$ summa gemensamma resistanser maska $i\neq j$ och där källorna i källvektorn $\mathbf{v}$ summeras positivt om de driver strömmen i referensriktningen, annars negativt)

$\left(\begin{array}{cc} 80 & -60 \\ -60 & 90 \end{array}\right)\left(\begin{array}{c} i_1 \\ i_2 \end{array}\right)=\left(\begin{array}{c} -8 \\ -37 \end{array}\right)$

Vilket ger oss lösningarna $i_1=-\frac{49}{60}\mathrm{A}$, $i_2=-\frac{43}{45}\mathrm{A}$. Därmed erhåller vi slutligen

$i_a=i_1\approx -0.82\mathrm{A}$

$i_b=i_2\approx -0.96\mathrm{A}$

$i_c=i_2+0.3\mathrm{A}\approx -0.66\mathrm{A}$