Kraftmoment
Hejsan
Jag har en fråga som jag är inte riktigt säker på.
Ett paket ställs i den högra änden av en homogen planka som är 4,5 m lång. Plankans tyngd är 11 kg medan paketets tyngd är okänd. Hur mycket kan paketet max väga utan att få plankan att välta?
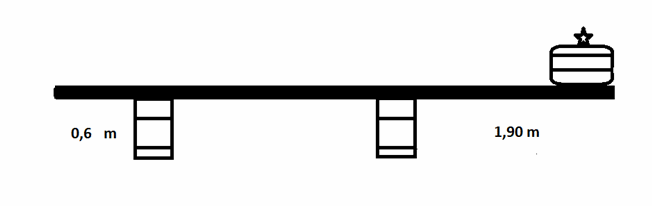
Jag gjorde så här:
Jag valde momentpunkten vid den vänstra balken, kraften F2 har ingen moment. Sedan beräknade jag sträckan från vridpunkt till masscentrum som blev 1,65 m.
Sedan sträckan från den vänstra balken till den högra som blev 2 m. Jag har ritat så här:

Jag vet också att enligt moment lagen gäller att:
Momenten medurs = Momenten moturs.
Därefter vet jag inte hur jag ska ta reda på paketets massa.
Kan ni vara snälla och hjälpa mig med den frågan?
Om paketet är för tungt, hur rör sig plankan då?
Den rör sig medurs.
Ja, genom att rotera runt det högra stödet.
Det säger något om krafterna i stöden.
Ursäkta men jag har inte riktigt förstått. Blir det rätt om jag gör så här:
Paket går medurs medan plankan går moturs, vilket blir :
Fg * (4,5 - 1,9) = Fg * 1,9 →
11 * 9,82 * 2,6 = m * 9,82 * 1,9 ?
När paketet är så tungt att plankan nästan tippar över, balanserar den på högra stödet. Kraften på vänstra stödet är då noll.
Är du med på det? Lägg en penna på ett par stöd och tryck ned ena änden, så blir det nog tydligt.
Paketet ger ett moment medurs, plankans tyngdkraft ett moturs.
jaha, nu tror jag att jag förstår vad du menar med krafterna i stödet.
Blir det rätt så då?
Fg * 1,9 = Fg * (4,5 - 1,9)
m * 9,82 * 1,9 = 11 * 9,82 * 2,6
osrrgh skrev:jaha, nu tror jag att jag förstår vad du menar med krafterna i stödet.
Blir det rätt så då?
Fg * 1,9 = Fg * (4,5 - 1,9)
Nej, här står ju att 1.9 = 2.6
m * 9,82 * 1,9 = 11 * 9,82 * 2,6
Nu är du på rätt väg, men har inte riktigt rätt hävarm.
Om jag tar L1= sträckan mellan momentpunkten och masscentrum = 1,65
Och L2= sträckan mellan vänstre och högra balken = 2
Utifrån momentlagen blir det:
m * 9,82 *2 = 11 * 9,82 * 1,65
blir det korrekt nu?
Nej, det vänstra stödet saknar betydelse här. Krafterna angriper i plankans masscentrum och längst till höger(paketet).
Räkna moment runt rotationscentrum, dvs högra stödet.
En kraft uppåt vid höger stöd, såklart. Den glömde jag.
Mmedurs= m * 9,82 * (2,25- 1,9) → längden blir då från höger stöd till masscentrum.
Mmoturs=11 * 9,82 * 2,25 → Längden blir här från paketet till masscentrum.
Ursäkta men jag såg olika exempel där längder väljs ut på olika sätt därför har jag svårt med det.
osrrgh skrev:Ursäkta men jag såg olika exempel där längder väljs ut på olika sätt därför har jag svårt med det.
Man kan välja origo för momentberäkningar var som helst, men det är ofta smartast att välja ett stöd (eller gångjärn osv).
Sedan är det bra att kolla sin uträkning med en momentberäkning kring ett annat rotationscentrum.
osrrgh skrev:Mmedurs= m * 9,82 * (2,25- 1,9) → längden blir då från höger stöd till masscentrum.
Mmoturs=11 * 9,82 * 2,25 → Längden blir här från paketet till masscentrum.
Ursäkta men jag såg olika exempel där längder väljs ut på olika sätt därför har jag svårt med det.
Blir det rätt i så fall?
Om jag sätter Mmedurs = Mmoturs
m * 9,82 * (2,25- 1,9) = 11 * 9,82 * 2,25
Jag har nu gjort så här:
11 * 9,82 * 1,65 = (m * 9,82 * 2,25)+ (FN2 *0,35)
Så du har en ekvation med två obekanta.
Då gissar jag att du inte har använt kraftjämvikt: allmänt gäller att summan av alla krafter är noll.
Men här är det lite enklare: man vet att kraften på stödet på andra sidan är noll.
Men hur ska jag annars göra i så fall?
osrrgh skrev:Men hur ska jag annars göra i så fall?
I din ritning finns FN1. Men den är noll när plankan är på gränsen till att välta.
Som även Bubo skrev.
Och FN2 då? som kommer från det högra stödet.
osrrgh skrev:Och FN2 då? som kommer från det högra stödet.
Den bidrar inte till något moment kring vridpunkten, som är ju det högra stödet.
Gör en tydlig ritning, med avstånden till vridpunkten tydligt angivna.
Nej, du lade inte en riktig penna på stöd, eller hur?
Hur vrider den sig? Vilken är punkten den vrider sig kring?
Ska jag istället göra så som nedan?
avståndet från paketet till masscentrum som är 2,25 m multipliceras med paketets massa* g , detta är Mmedurs
plankans tyng * g * avståndet från masscentrum till det högra stödet som är 0,35, detta är Mmoturs
Innan du börjar räkna med bara siffror är det bra att fundera på hur den här plankan egentligen rör sig.
Den ligger på två stöd, och paketet trycker på den biten som sticker ut till höger. Hur vrids då plankan, när paketet är tillräckligt tungt? Du behöver bara lägga en penna på två stöd och trycka till, så ser du det direkt.
Den kommer att vrida sig medurs kring högra stödet.
osrrgh skrev:Den kommer att vrida sig medurs kring högra stödet.
Ja, just det!

Då blir det så, eller hur:
1,9 * m *g = 11 * 9,82 * 0,35
Ja, nu stämmer det.
Kraften i det vänstra stödet är noll precis när plankan är på väg att lyfta där.
Du har skrivit 9.82 på ett ställe och g på ett annat ställe. Skriv samma, så ser du att du kan förenkla ekvationen.
Ok, tusen tack för er hjälp.
En fråga bara: Tryckte du på en penna på riktigt, eller tänkte du noga?
Jag gjorde det på riktigt
Bra! Visst blir det väl lättare då?
(Jag försökte få dig att göra det redan i onsdags morse...)
Stämmer, tack för dig.



