Kraftmoment
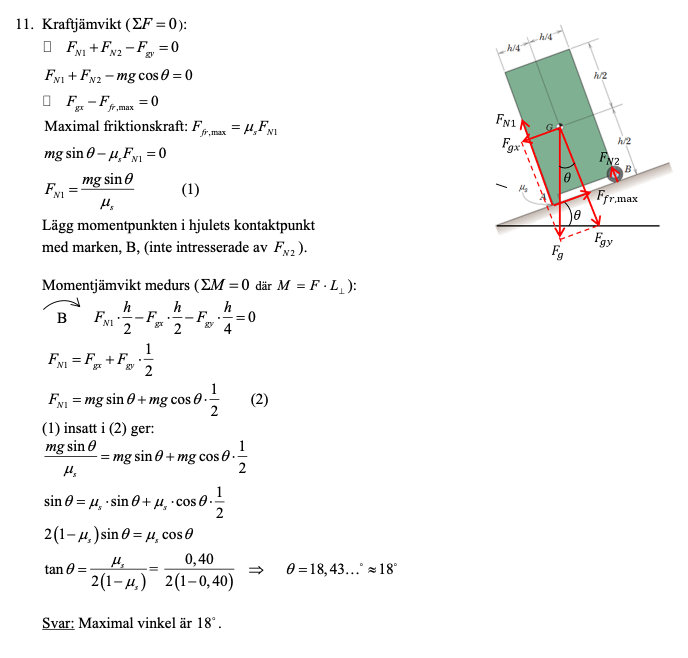
Man ska beräkna maximala vinkeln theta för vilket soptunnan inte glider, mina beräkningar är likadana som facit förutom att de har räknat med x-komposanten för tyngdkraften i momentjämviktsekvationen och det gjorde jag inte men förstår inte varför de gör det, det är väl endast den rätvinklade komposanterna mot momentpunkten som verkar?
Kan du lägga in en bild av själva frågan också, så att vi slipåper gissa vad det är man frågar efter?
Smaragdalena skrev:Kan du lägga in en bild av själva frågan också, så att vi slipåper gissa vad det är man frågar efter?

tjohej2005 skrev:...de har räknat med x-komposanten för tyngdkraften i momentjämviktsekvationen och det gjorde jag inte men förstår inte varför de gör det, det är väl endast den rätvinklade komposanterna mot momentpunkten som verkar?
Jag förstår inte vad du menar. Du verkar ha missförstått något. "x-komposanten" (rött) har rät vinkel till sin hävarm (orange) vid skärningspunkten med kraftens verkningslinje:

Hur menar du att den inte är en del av de "rätvinklade komposanterna"?
Ebola skrev:tjohej2005 skrev:...de har räknat med x-komposanten för tyngdkraften i momentjämviktsekvationen och det gjorde jag inte men förstår inte varför de gör det, det är väl endast den rätvinklade komposanterna mot momentpunkten som verkar?
Jag förstår inte vad du menar. Du verkar ha missförstått något. "x-komposanten" (rött) har rät vinkel till sin hävarm (orange) vid skärningspunkten med kraftens verkningslinje:
Hur menar du att den inte är en del av de "rätvinklade komposanterna"?
Jag tänkte som följande och då blir den istället parallell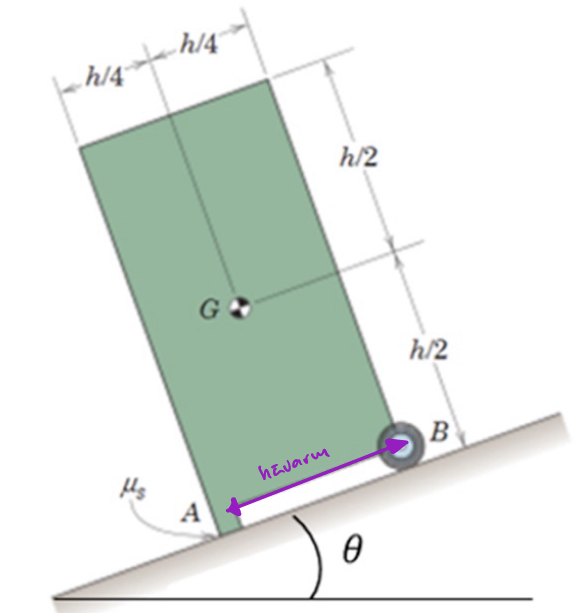
Förstod nu när du ritade upp det varför man räknar med x-komponsanten. Dock uppkommer det andra problem för mig då.
1. De räknar inte med som också verkar i samma riktning som tyngdkraftens x-komposant fast motsatt (den är också vinkelrät), är det för att den verkar i vridningscentrum?
2. Hur vet man att momentarmen skall vara vertikalt så som du illustrerade och inte horisontell som på bilden jag infogade?
3. Om momentarmen är vertikal på samma sätt som du illustrerade, då kommer väl inte vara vinkelräta längre mot hävarmen utan istället parallella och därmed inte utöva ett moment?
Säg gärna till om jag har beskrivit något otydligt.
tjohej2005 skrev:1. De räknar inte med som också verkar i samma riktning som tyngdkraftens x-komposant fast motsatt (den är också vinkelrät), är det för att den verkar i vridningscentrum?
Hävarmen för är lika med noll. Alltså skär kraften "vridningscentrum" eller momentpunkten i hjulets kontaktpunkt med marken B.
2. Hur vet man att momentarmen skall vara vertikalt så som du illustrerade och inte horisontell som på bilden jag infogade?
Hävarmen kan inte vara parallell med kraften. Den måste vara vinkelrät till kraften per definition. Då är parallell med det lutande planet måste hävarmen vara normal till det lutande planet eller "vertikalt", som du kallar det.
3. Om momentarmen är vertikal på samma sätt som du illustrerade, då kommer väl inte vara vinkelräta längre mot hävarmen utan istället parallella och därmed inte utöva ett moment?
De har sina egna separata hävarmar som skiljer sig från varandra samt den för .
- Hävarmen för är parallell med planet och lång.
- Hävarmen för är parallell med planet och lång.
- Hävarmen för är normal till planet och lång.
Ebola skrev:tjohej2005 skrev:1. De räknar inte med som också verkar i samma riktning som tyngdkraftens x-komposant fast motsatt (den är också vinkelrät), är det för att den verkar i vridningscentrum?
Hävarmen för är lika med noll. Alltså skär kraften "vridningscentrum" eller momentpunkten i hjulets kontaktpunkt med marken B.
2. Hur vet man att momentarmen skall vara vertikalt så som du illustrerade och inte horisontell som på bilden jag infogade?
Hävarmen kan inte vara parallell med kraften. Den måste vara vinkelrät till kraften per definition. Då är parallell med det lutande planet måste hävarmen vara normal till det lutande planet eller "vertikalt", som du kallar det.
3. Om momentarmen är vertikal på samma sätt som du illustrerade, då kommer väl inte vara vinkelräta längre mot hävarmen utan istället parallella och därmed inte utöva ett moment?
De har sina egna separata hävarmar som skiljer sig från varandra samt den för .
- Hävarmen för är parallell med planet och lång.
- Hävarmen för är parallell med planet och lång.
- Hävarmen för är normal till planet och lång.
Hur vet man vilka av krafterna som uträttar moment moturs/medurs?
tjohej2005 skrev:Hur vet man vilka av krafterna som uträttar moment moturs/medurs?
Genom vad moturs/medurs betyder... Läs här:
https://fysikguiden.se/kraftmoment/
När en kraft verkar genom att rotera något medurs har kraftmomentet riktning medurs. Rita en cirkel med centrum där du beräknar momentet:

Du ser här att kraften i rött har en verkningslinje (det streckade) som tangerar den blå cirkeln. Eftersom kraften i denna punkt har riktning snett ned åt vänster betyder detta att kraften verkar med ett moturs kraftmoment kring punkten B.
Tillägg: 5 jan 2022 16:26
Du ser annars här normalkraften i nedre vänstra hörnet som utövar ett medurs kraftmoment:

Ebola skrev:tjohej2005 skrev:Hur vet man vilka av krafterna som uträttar moment moturs/medurs?
Genom vad moturs/medurs betyder... Läs här:
https://fysikguiden.se/kraftmoment/
När en kraft verkar genom att rotera något medurs har kraftmomentet riktning medurs. Rita en cirkel med centrum där du beräknar momentet:
Du ser här att kraften i rött har en verkningslinje (det streckade) som tangerar den blå cirkeln. Eftersom kraften i denna punkt har riktning snett ned åt vänster betyder detta att kraften verkar med ett moturs kraftmoment kring punkten B.
Blir det då att är medurs och moturs?
tjohej2005 skrev:Blir det då att är medurs och moturs?
Japp. Tänk också på att om cirkeln tangerar kraften eller dess verkningslinje kommer cirkelns radie vara lika med hävarmens längd.
Om du inte vet vad tangerar betyder kan du läsa om det här:
http://www.malinc.se/math/geometry/dothissv.php
Det betyder helt enkelt att en linje som tangerar en cirkel är vinkelrät till radien på cirkeln:

Ebola skrev:tjohej2005 skrev:Blir det då att är medurs och moturs?
Japp. Tänk också på att om cirkeln tangerar kraften eller dess verkningslinje kommer cirkelns radie vara lika med hävarmens längd.
Om du inte vet vad tangerar betyder kan du läsa om det här:
http://www.malinc.se/math/geometry/dothissv.php
Det betyder helt enkelt att en linje som tangerar en cirkel är vinkelrät till radien på cirkeln:
Okej! Då förstår jag :D
Bara för att vara helt säker, är detta korrekt?
Alla krafter som verkar på ett föremål och som inte går igenom vridningscentrum utövar ett moment och dessa krafter har alla en hävarm som är det vinkelräta avståndet till vridningscentrum.
tjohej2005 skrev:Alla krafter som verkar på ett föremål och som inte går igenom vridningscentrum utövar ett moment och dessa krafter har alla en hävarm som är det vinkelräta avståndet till vridningscentrum.
Helt korrekt. Ett par tillägg bör dock göras:
- Om ett objekt är i jämvikt kommer summan av alla kraftmoment bli noll oavsett vilken punkt du väljer som momentpunkt, även utanför strukturen. Därmed existerar inget bestämt "vridningscentrum" och momentpunkten kan väljas godtyckligt.
- Du kan därför välja den momentpunkt att studera som förenklar beräkningarna. Exempelvis sådana där hävarmen för krafter du inte är intresserad av att bestämma är lika med noll. I uppgiftens lösningsförslag valde de momentpunkt i B då de tyckte att normalkraften i B var ointressant. Du kunde istället valt momentpunkt i A men då hade uppgiften blivit lite längre.
Ebola skrev:tjohej2005 skrev:Alla krafter som verkar på ett föremål och som inte går igenom vridningscentrum utövar ett moment och dessa krafter har alla en hävarm som är det vinkelräta avståndet till vridningscentrum.
Helt korrekt. Ett par tillägg bör dock göras:
- Om ett objekt är i jämvikt kommer summan av alla kraftmoment bli noll oavsett vilken punkt du väljer som momentpunkt, även utanför strukturen. Därmed existerar inget bestämt "vridningscentrum" och momentpunkten kan väljas godtyckligt.
- Du kan därför välja den momentpunkt att studera som förenklar beräkningarna. Exempelvis sådana där hävarmen för krafter du inte är intresserad av att bestämma är lika med noll. I uppgiftens lösningsförslag valde de momentpunkt i B då de tyckte att normalkraften i B var ointressant. Du kunde istället valt momentpunkt i A men då hade uppgiften blivit lite längre.
Okej! Tack så mycket :D



