Kraftkomposant, vektorer, Q1, 2021
Jag är ju helt lost. Hur löser jag komposant-problem med vinklar större än 90 grader? Och hur vet jag vilken vektor som är 100N?


Det borde stå att det hela ska vara i jämvikt, annars kan man inte avgöra någonting.
Laguna skrev:Det borde stå att det hela ska vara i jämvikt, annars kan man inte avgöra någonting.
Mmh, tänkte det också. Hur gör jag ifall den är i jämvikt? Min metod känns kass
Jag förstår inte riktigt din figur. Det verkar som om du har missuppfattat repens riktning.
Rita en ny figur där du kallar repen R1, R2 och R3.
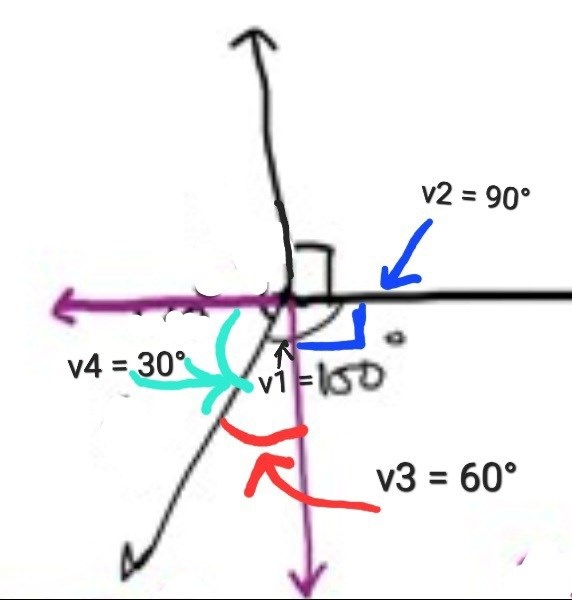
- Vinkeln mellan R1 och R2 är 90°
- Vinkeln mellan R2 och R3 är 120°
- Vinkeln mellan R3 och R1 är 150°
Yngve skrev:Jag förstår inte riktigt din figur. Det verkar som om du har missuppfattat repens riktning.
Rita en ny figur där du kallar repen R1, R2 och R3.
- Vinkeln mellan R1 och R2 är 90°
- Vinkeln mellan R2 och R3 är 120°
- Vinkeln mellan R3 och R1 är 150°

Vad gör jag nu?
Bra.
Nästa steg kan vara att försöka klura ut vilket av repen som det dras i med 100 N. Du har skrivit att det är R2, men det kan inte stämma. Om du inte kan klura ut varför, så klicka på tipsen:
Tips 1
Kraftsumman ska vara lika med 0 eftersom det råder jämvikt.
Tips 2
De andra två krafterna är mindre än 100 N, så de måste på något sätt hjälpas åt att balansera kraften på 100 N.
Tips 3
I detta sammanhang är det något speciellt med de två rep som bildar vinkeln 90° mot varandra.
Yngve skrev:Bra.
Nästa steg kan vara att försöka klura ut vilket av repen som det dras i med 100 N. Du har skrivit att det är R2, men det kan inte stämma. Om du inte kan klura ut varför, så klicka på tipsen:
Tips 1
Kraftsumman ska vara lika med 0 eftersom det råder jämvikt.
Tips 2
De andra två krafterna är mindre än 100 N, så de måste på något sätt hjälpas åt att balansera kraften på 100 N.
Tips 3
I detta sammanhang är det något speciellt med de två rep som bildar vinkeln 90° mot varandra.
Okej, jag kom fram till att R1 är 100N. Vad gör jag sedan?
Nej det kan inte stämma.
Nu kallar jag krafterna F1, F2 och F3 för att inte förväxla krafter med rep.
Den enda kraft som kan balansera F1 i horisontell ledd är F3 eftersom F2 inte har någon komposant i horisontell ledd.
F3s komposant i horisontell ledd är mindre än F3 själv, vilket betyder att F3 > F1.
På samma sätt går det att resonera sig fram till att F3 > F2.
Hängde du med på det?
Om inte - dela upp F3 i en horisontell och en vertikal komposant med hjälp av trigonometri och ställ upp de två jämviktsekvationerna för de ingående krafterna så framgår ovanstående även algebraiskt.
Kanske följande figur ger vissa insikter.

Yngve skrev:Nej det kan inte stämma.
Nu kallar jag krafterna F1, F2 och F3 för att inte förväxla krafter med rep.
Den enda kraft som kan balansera F1 i horisontell ledd är F3 eftersom F2 inte har någon komposant i horisontell ledd.
F3s komposant i horisontell ledd är mindre än F3 själv, vilket betyder att F3 > F1.
På samma sätt går det att resonera sig fram till att F3 > F2.
Hängde du med på det?
Om inte - dela upp F3 i en horisontell och en vertikal komposant med hjälp av trigonometri och ställ upp de två jämviktsekvationerna för de ingående krafterna så framgår ovanstående även algebraiskt.
Tack, nu hänger jag med på vilken som är störst. Det blir ändå konstigt när jag vill få fram storleken, komposanterna blir inte 100N tillsammans. Varför blir detta fel?

Om du vektoradderar krafterna kommer den sammanlagda kraften att ha rätt storlek (och en riktning motsatt R3).
Först ett räknefel, det gäller att , inte .
Sedan ska det inte gälla att Rv + Rh = R3 utan istället att Rv2 + Rh2 = R32 enligt Pythagoras sats.
Jag vet inte hur man har kommit fram till vinklarna 30 och 60 grader som bildar 90 grader, hur och varför har man delat upp dem på det sättet?
Eftersom v1 = 150° och v2 = 90° så måste v3 = 150°-90° = 60°. Eftersom v3+v4 = 90° så måste v4 = 30°
F1 = F1(1, 0).
F2 = F2(0, 1)
F3 = 100(cos(90 + 120), sin(90 + 120)) = 100(cos(30 + 180), sin(30 + 180)) =
-100(cos(30), sin(30)).
Jämvikt: F1 + F2 + F3 = 0.





