Kraften på varandra, hur tolkar man uppgifter
Jag blir väldigt förvirrad när jag läser uppgifter i elfält, jag vet inte hur jag ska tolka geometrin och frågan, så jag tänkte skriva några exempel och hur jag har tolkat de och undrar om det stämmer? Det gäller på fältstyrkan och kraften men framförallt frågor om kravet som objekt har tillsammans i en punkt eller på varandra eller från ett visst avstånd till varandra
a) två tunna stavar med längden L ligger längs motstående sidor i en kvadrat. Stavarna har belagts likformigt med laddningen av motsatt polaritet, med totalladdningen Q resp -Q. Beräkna den elektriska fältstyrkan i kvadratens mitt.
Här tänkte jag att man kanske kan använda symmetriargument och bara beräkna en integral för den positiva laddningen och sedan fördubbla det, däremot vet jag inte hur det blir med tecknet på laddningen, eller kan man inte använda symmetriargument alls?
b) två tunna stavar med längden L har totalladdningarna Q1 respektive Q2, jämnt fördelade längs stavarna. Beräkna den kraften, med vilken stavarna påverkar varandra, om de är placerade utefter en rät linje på det inbördes avståndet d.
Här vet jag absolut inte hur jag ska anpassa formeln till geometri, hur beräknar jag deras kraft på varandra? Är det så att jag räkna L+d på ena och sedan adderar med L+d med den andra, kan jag inte då beräkna ena integralen och fördubbla den?
c) två likadana tunna ebonitstavar, vardera med längden L har totalladdningarna Q1 respektive Q2, jämnt fördelade över stavarna. Beräkna kraften på stavarna om de är placerade i mitt för och parallelt med varandra på det inbördes avståndet d.
Är detta samma geometri som a fast vi vill ha kraften som de har på varandra? Hur får man fram det?
Hej!
Jag kan försöka svara hur jag skulle börja att angripa dina uppgifter. Men det kan ju mycket väl vara så att jag upptäcker att det måste finnas enklare sätt efter en stunds räknande, men hoppas det hjälper dig lite iallafall.
Symmetrier är nog det första jag funderar på, för att göra beräkningar så enkla som möjligt. Här är det stavar med jämn laddningsfördelning, men om man först tänker sig rader med punktformade laddningar så tycker jag det är lite enklare att se symmetrier, att en laddning på ett visst ställe på en stav, "tar ut" bidraget från en annan laddning, och på så sätt upptäcker man att man kan skippa en del beräkningar.
a) e-fältet i en punkt är kraften på en tänkt positiv enhetsladdning i den punkten. Jag tänker att om ena staven är positiv och andra staven är negativ (på motsatta sidan beräkningspunkten) så kommer vardera staven att bidra lika mycket till det totala efältet i punkten. Jag observerar också att i en ledd är det samma laddningsfördelning på båda sidor om punkten, så totala fältet borde bli noll i den ledden.
b) Jag vet inte om det finns någon bra symmetri här. Jag skulle försöka titta på hur stor kraft som en av stavarna påverkar en liten del dL av den andra staven, och sedan integrera över den andra stavens längd för att få totala kraften.
c) Samma uppställning som a som du säger. Beräkna totala kraften som i b. Utnyttja symmetrin på samma sätt som i a.
Nichrome skrev:frågor om kravet som objekt har tillsammans i en punkt eller på varandra eller från ett visst avstånd till varandra
Jag förstår inte riktigt.
Men det är väl bara att börja? Till exempel rita en tolkning av geometrin.
Här finns en länk för hjälp med att visualisera fält.
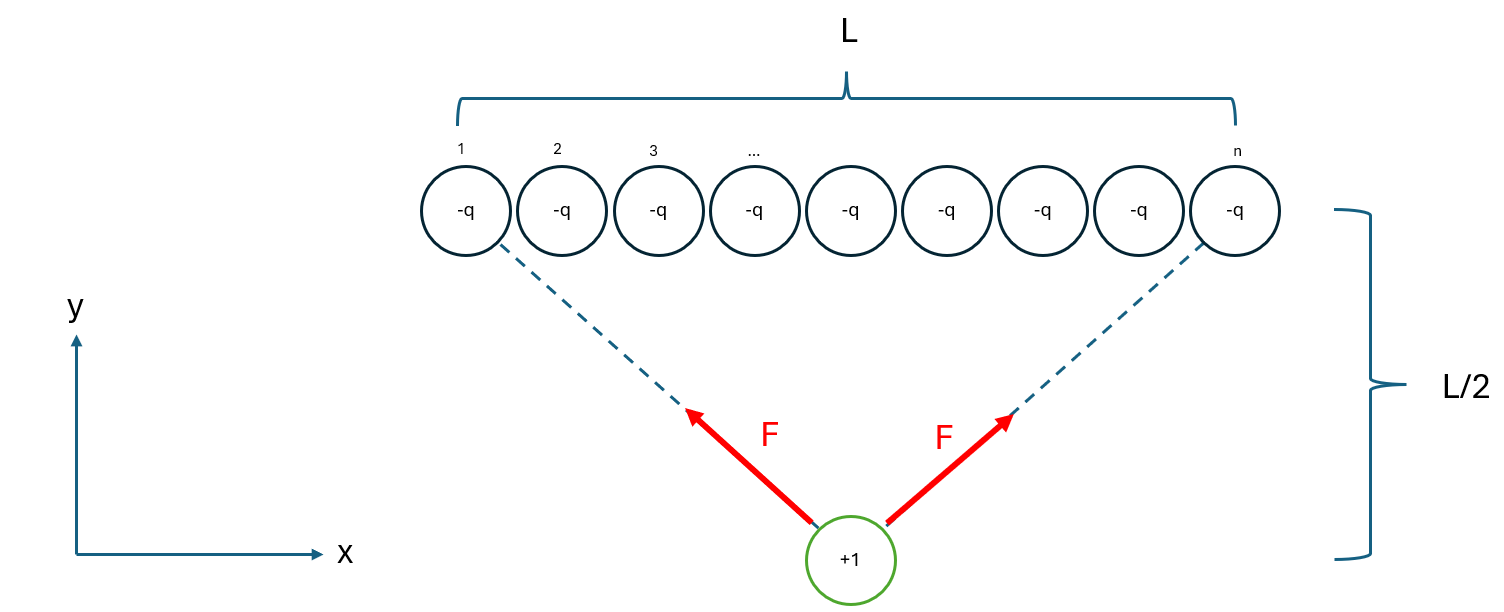
Lite om symmetri och e-fält och hur jag tänker i a). Jag tänker mig (först) staven som en radda punktladdningar, dvs diskretiserar uppgiften, tycker det är lättare att tänka så. Jag sätter ut en enhetsladdning där jag vill beräkna fältstyrkan. Ganska snart ser jag att coulombkrafterna som testladdningen utsätts för från laddning nr 1 och nr n kommer att ta ut varandra i x-led. Samma sak gäller om man tittar på krafterna från laddning nr 2 och nr n-1, nr 3 och n-2 osv osv ända tills man kommer till mitten av staven. Alltså behöver jag inte ens bry mig om att beräkna någon summakraft i x-led tack vare symmetrin (se också Pieters figur ovanför, vilken bekräftar att ingen fält finns i x-led i den punkten).
Tittar jag på krafter i y-led så ser jag att krafterna som testladdningen utsätts för från laddning nr 1 och nr n är lika stora. Samma sak gäller om man tittar på krafterna från laddning nr 2 och nr n-1, nr 3 och n-2 osv osv ända tills man kommer till mitten av staven. Alltså, för att beräkna summakraften i y-led skulle jag bara behöva integrera över ena halvan av staven och sedan multiplicera med 2, tack vare symmetrin.