Kraftekavtion

Maria123 skrev:

Hej,  nör jag ställer upp kraftekvationen i en: riktningen vid punkten A får jag inte samma svar som facit. Enligt facit ör mg:s en:komponent lika med mg/rotenur(2) medan jag får mg:s en:komponent till mg gånger rotenur(2).

Facit:

Min början på lösningen: 

Om du delar upp en kraft i sina komposanter, och den ena komposanten är större än själva kraften, så har du gjort något fel. Rita in "dina" komposanter och lägg upp bilddn på nytt.

Eller kanske rättare sagt såhär. Kan man säga då att varje gång man delar upp en kraft i dess komposanter bör man frilägga så att kraften utgör ”hypotenusan” i friläggningen? Kan det vara en tumregel?

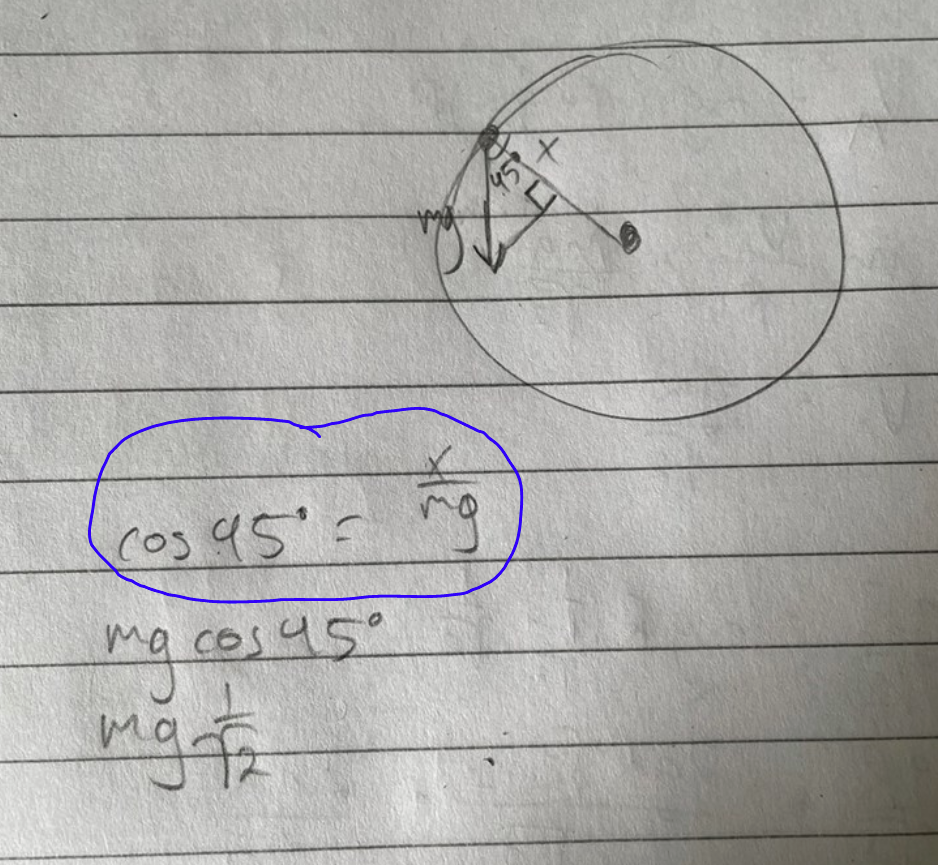
Jag funderar på det inringade uttrycket.
cos(45) är dimensionslös men x/mg är inte dimensionslös, väl?

Känns som det hänt något skumt här.

Både kraften x och kraften mg mäts i newton. Då blir kvoten mellan dem dimensionslös.

Ah, jag trodde x var en längd. (Tidigare stod det R/mg, det lurade mig lite).