Kraft
Hej!
jag förstår inte hur den här linan kan vara balanserad när pappan håller upp den. Jag resonerar så som den andra bilden nedan

Jag tror vi får anta att brädan i sig är balanserad. Dvs den har sin tyngdpunkt vid stödet så där får vi brädans tyngdkraft, 30*9.82N, och en motriktad kraft från stödet på lika mycket.
Pappans kraft uppåt på 130N motsvarar Petters tyngdkraft så balans råder fortfarande.
Hej men Peters tyngd motsvarar 255 N nedåt medan pappans kraft är 130 N uppåt så då balanseras de väl inte?
Hävarmens längd, dvs avståndet från resp kraft till vridningspunkten har också betydelse
Tänk på att momentet = kraft*hävarmslängd, och det är momentet som måste vara i jämnvikt för att brädan inte ska vrida sig runt stödet. (Givetvis måste det också vara kraftjämnvikt, två krafter känner vi till, den tredje är vid brädans stödpunkt, den kan vi räkna ut)
Men isåfall om man sätter två olika vikter på varsin ände så borde den också vara i jämvikt då den tredje kraften kommer från stödpunkten?
Ture skrev:Hävarmens längd, dvs avståndet från resp kraft till vridningspunkten har också betydelse
Tänk på att momentet = kraft*hävarmslängd, och det är momentet som måste vara i jämnvikt för att brädan inte ska vrida sig runt stödet. (Givetvis måste det också vara kraftjämnvikt, två krafter känner vi till, den tredje är vid brädans stödpunkt, den kan vi räkna ut)
Men isåfall om man sätter två olika vikter på varsin ände så borde den också vara i jämvikt då den tredje kraften kommer från stödpunkten?
karam123 skrev:
Men isåfall om man sätter två olika vikter på varsin ände så borde den också vara i jämvikt då den tredje kraften kommer från stödpunkten?
Ja, men om det är momentjämvikt eller inte beror på hur tunga vikterna är och var de placeras.
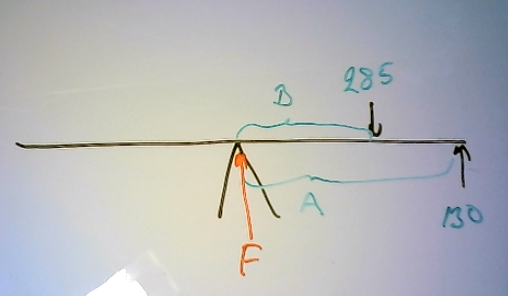
Titta på bilden nedan
För att det ska vara momentjämnvikt måste
B*285 = A*130 alltså medurs moment = moturs moment
För att det ska vara kraftjämnvikt måste
F+130 = 285 (jag har för enkelhets skull struntat i brädans vikt) dvs uppåtriktade krafter = nedåtriktade krafter