Kovergerar integralen?
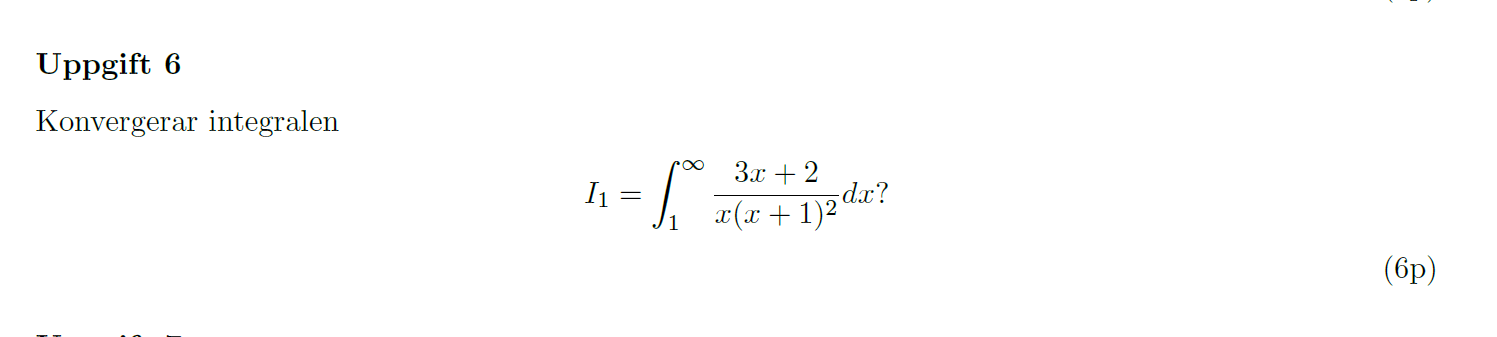
I facit säga det:

Varför kan man jämföra med hjälp av jämförelsessatsen.
Du har glömt en tvåa i (x+1)2 i nämnaren.
Laguna skrev:Du har glömt en tvåa i (x+1)2 i nämnaren.
Slarv fel.

Varför delar de med 1/x^2 i facit?
För att de har observerat att integranden beter sig som 1/x2 för stora värden på x.
Laguna skrev:För att de har observerat att integranden beter sig som 1/x2 för stora värden på x.
Hur vet man att integraden bete som ???
För att täljaren har gradtalet 1 och nämnaren 3. 3-1 = 2.
Laguna skrev:För att täljaren har gradtalet 1 och nämnaren 3. 3-1 = 2.
Täljaren har gradtalet 1 det hänger ja med.
Men vad menar du med "nämnaren 3.3-1=2"??
Nämnaren har gradtalet 3 (och täljaren har gradtalet 1).
Om vi bryter ut x i båda leden och förkortar bort det, får vi kvar 1 (+ lite krångel) i täljaren och x2 (och lite annat krångel) i täljaren, så kurvan kommer i stort sett att bete sig sim 1/x2 när x går mot oändligheten. Både "lite krångel" och "lite annat krångel" går mot 0 när x går mot oändligheten.
Marcus N skrev:Laguna skrev:För att täljaren har gradtalet 1 och nämnaren 3. 3-1 = 2.
Täljaren har gradtalet 1 det hänger ja med.
Men vad menar du med "nämnaren 3.3-1=2"??
Punkten är slut på en mening. Nästa mening lyder "3-1=2".
Om x är stort så får vi att täljaren är .
I nämnaren har vi men om är godtyckligt stort så får vi att
nämnaren blir alltså . Vi har nu och konstanten är inte så himla viktigt. Vi ser nu att för stora så vi ett beteende liknande
Dracaena skrev:Om x är stort så får vi att täljaren är .
I nämnaren har vi men om är godtyckligt stort så får vi att
nämnaren blir alltså . Vi har nu och konstanten är inte så himla viktigt. Vi ser nu att för stora så vi ett beteende liknande
Nu fattar ja helt.





