Konvergensskiva och komplex integral

Hej! Sitter med gamla tentor och har stött på en uppgift, retligt då jag får fram ett svar som är fel med en faktor 2.
Upp giften är:
Jag började med att använda kvotkriteriet på serien:
$ρ = \lim_{k \to \infty} {|\frac{k^{2}}{5^{k}} {(2 z - i)}^{k}|}^{\frac{1}{k}} = 2 |z - \frac{i}{2}| \lim_{k \to \infty} |\frac{k^{\frac{2}{k}}}{5}| = 2 |z - \frac{i}{2}| \lim_{k \to \infty} |\frac{e^{\frac{2 \ln k}{k}}}{5}| = \frac{2}{5} |z - \frac{i}{2}|$

Det ger att vi har en konvergensskiva:
$|z - \frac{i}{2}| < \frac{5}{2}$

Sen tänkte jag att man kunde använda Taylors sats om holomorfa funktioner i samband med Cauchys integralformel för att räkna ut integralen.
Skriver man om Cauchys integralformel så får man:

$2 π i \frac{f^{(k)} (p)}{k!} = \int_{C} \frac{f (z)}{{(z - p)}^{k + 1}} d z$

Sen tänkte jag nyttja det faktum att vi hittat konvergensskivan, cirkeln $|z| = 1$ ryms helt och hållet på konvergensskivan. Så jag tänkte att man kunde nyttja följden av Taylors sats(Löst citerat) :
Går f att skriva som en potensserie centrerad i c:

$f (z) = \sum_{k = 0}^{\infty} a_{k} {(z - c)}^{k}$
tillsammans med cauchys integralsats så blir a_k:
$a_{k} = \frac{f^{k} (z)}{k!}$

Alltsom allt då
$\int_{|z| = 1} \frac{f (z)}{{(2 z - i)}^{4}} d z = 2 π i \frac{f^{(3)} (i)}{3!} = 2 π i a_{3} = 2 π i \frac{3^{2}}{5^{3}} = \frac{18 πi}{125}$

Facit ger $\frac{9 πi}{125}$ och föreslår att man ska använda residykalkyl med regeln: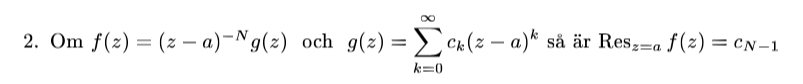
Men då måste man ju multiplicera resultatet med $2 π i$ vilket jag ändå får till $\frac{18 πi}{125}$ .

Har jag stirrat mig helt blind här och missat någon detalj!

Tack så mycket på förhand!

Edit: skrivit en siffra fel.

Jag ser inte heller några större fel, särskilt som du dubbelkollar mot residusatsen och tänker på faktorn 2pi i. Emellertid var det längesen jag var i det holomorfa, så viss reservation!

Då vi delar potensserien med faktorn $(2z-i)^4=2^4(z-i/2)$ inser vi att den intressanta termen i Laurentutvecklingen inträffar då $k=3$ . Termen blir

$\displaystyle \frac{3^22^3(z-i/2)^3}{5^32^4(z-i/2)^4}=\frac{3^2}{125\cdot 2 (z-i/2)}$

Alltså är den sökta koefficienten (residuen) $\mathrm{Res}[f(z), i/2]=c_{-1}=\frac{9}{250}$

Residuesatsen säger att

$\displaystyle \frac{1}{2\pi i}\oint_C f\left(z\right)\,dz=\sum_{j=1}^n\mathrm{Res}[f\left(z\right), z_j]$

Där $z_1,z_2,\dots, z_n$ är singulariteterna inom ett av kurvan $C$ enkelt sammanhängande omslutet område där $f(z)$ i övrigt är analytisk. Vi har endast en singulär punkt $z_1=i/2$ och vår sökta integral blir därmed

$\displaystyle \oint_{|z|=1} f\left(z\right)\,dz=2\pi i \cdot \frac{9}{250}=\frac{9\pi i}{125}$

Ahh jag ser, jag använd z=i som pol istället för z= i/2. Samt missade faktorn i potensserien. Laurentserier täcks inte av kursen. Borde väl gå med taylorssats och cauachys integrlformel med. Testade lite löst verkar ge samma resultat.

Svara

Visa senaste svar