Kontinuitet och gränsvärden
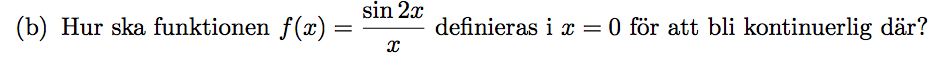
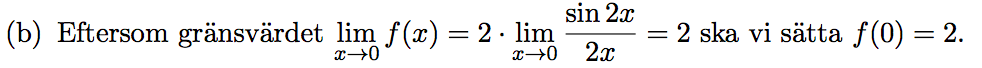Jag förstår inte hur man får fram att gränsvärdet är 2?? Jag vet ju att sin2x = 2sinxcosx, men det är ju noll när x -> 0 samt att det står ju fortfarande x i nämnaren så man kan inte dela med noll. Jag vet att en funktionen är kontinuerlig i x=0 om gränsvärdet när x -> 0 är samma som funktionsvärdet i x=0. Jag förstår verkligen inte hur de har gjort, så det skulle uppskattas om någon kan förklara
är ett standardgränsvärde som förekommer rätt så ofta, bra att memorera det. Du kan även skriva om bråket som och byta ut mot exempelvis, då får du som när du tar gränsvärdet mot 0 också blir 1 enligt standardgränsvärdet. I din uppgift, för att utnyttja standardgränsvärdet så måste det inom parenteserna i sin vara samma som det i nämnaren, för att detta ska vara möjligt kan du förlänga med , sedan bryter de bara ut 2 ur gränsvärdet och har kvar 1/2 i gränsvärdet
Okej, jag förstår! Men kan man också då räkna att
Och så vet man att 2cos(0)= 2 när x -> 0 och med standardgränsvärdet sin(x)/x=1 när x-> 0, blir det 2, och då måste funktionsvärdet f(0) = 2, för att den ska vara kontinuerlig.
