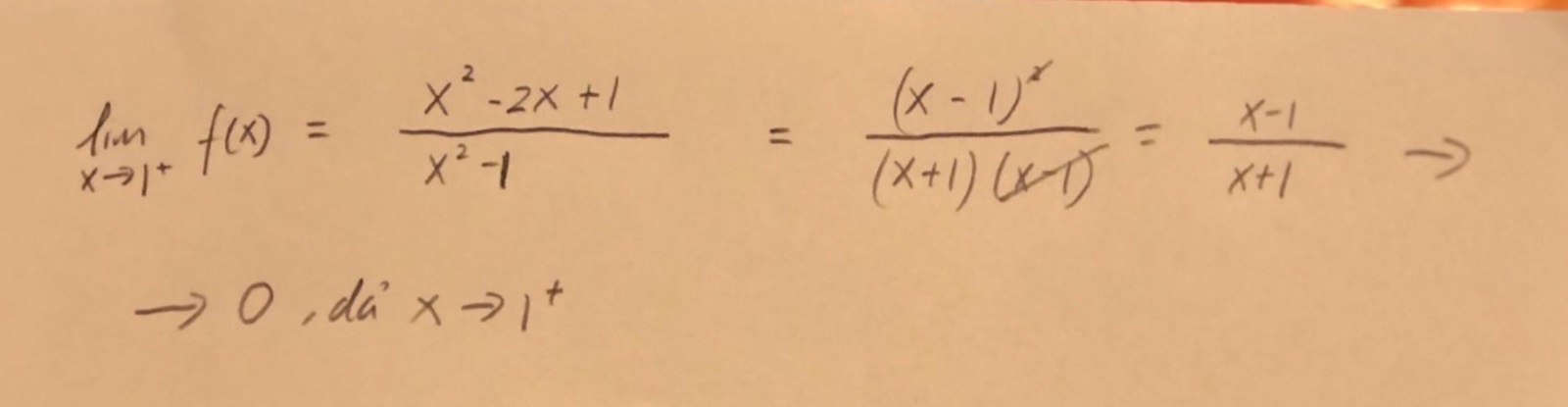Kontinuitet

Har du testat att faktorisera $\frac{x^2-2x+1}{x^2-1}?$

Uträkning ger a=-1, b=1.

Men för att funktionen ska vara kontinuerligt så måste funktionens värde vid punkten x=a alltså f(a) också lika med gränsvärde vid den samma punkten a.

$$\begin{gathered} a=-1, b=1 \\ f\left(0\right)=1 \\ f\left(1\right)=0. \\ Så det skulle visas. \end{gathered}$$

Hallå???

Inlägg #3 syns inte, så vi vet inte om du har svarat på ItzErres fråga.

Vilket gränsvärde har f(x) om man närmar sig 0 från vänster? (Du har helt korrekt svarat att det är 1.)

Vilket gränsvärde har f(x) om vi närmar oss 1 från höger? Det kan jag inte se att du har svarat på. Gränsvärdet existerar.

Då kan man konstruera en rät linje som går genom punkterna (0,1) och (1,0), alltså y = 1-x (d v s a = -1, b = 1) som du har skrivit i inlägg #4 (fast på ett sätt som var svårbegripligt, åtminstone för mig).

Är nästa fråga möjligen om man kan välja f(x) = ax+b i intervallet [0,1] så att f(x) är deriverbar i hela $\mathrm{ℝ}$?

Jo, jag håller med. Men jag har kommit fram till att a=-1 och b=1.

Marcus N skrev:

Jo, jag håller med. Men jag har kommit fram till att a=-1 och b=1.

Vad är det du håller med om? Att du har formulerat dig på ett svårbegripligt sätt? Jag håller med om att f(x) = -x+1 är den rätta räta linjen.

Nej, ja menar ja är överrens med dig.

Summering:

Sätt =-1, b=1 så är f(x) kontinuerligt på hela R.

Stämmer det?

Marcus N skrev:

Summering:

Sätt a=-1, b=1 så är f(x) kontinuerligt på hela R.

 

Stämmer det?

Ja, med den korrigeringen jag gjorde.

$Menar du f\left(x\right)=-x+1, x\in \left[0,1\right]$

Hallå? Ni har inte svarat på den sista inlägg så ja antar jag har tänkt rätt.