Kontinuerlig förlängning

Att försöka rita är alltid bra! :)

För att funktionen ska vara kontinuerlig får det inte finnas något "glapp" i funktionen. På matematiska innebär det att det måste gälla att $\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }f\left(x\right)=f\left(2\right)$. 

Värdet av $f(2)=2^2=4$, eftersom $f(x)$ definieras som $x^2$ då $x=2$. Från höger påväg till $x=2$ har vi en och samma funktionsuttryck, $f(x)=x^2$, som är ett polynom. Polynomfunktioner är alltid kontinuerliga, om inget annat anges. Därför behöver vi inte bry oss om högergränsvärdet – brottet i funktionen kommer först efter $x=2$, om vi kommer från höger. 

Vad blir gränsvärdet från vänster? :)

Smutstvätt skrev:

Att försöka rita är alltid bra! :)

För att funktionen ska vara kontinuerlig får det inte finnas något "glapp" i funktionen. På matematiska innebär det att det måste gälla att $\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }f\left(x\right)=f\left(2\right)$. 

Värdet av $f(2)=2^2=4$, eftersom $f(x)$ definieras som $x^2$ då $x=2$. Från höger påväg till $x=2$ har vi en och samma funktionsuttryck, $f(x)=x^2$, som är ett polynom. Polynomfunktioner är alltid kontinuerliga, om inget annat anges. Därför behöver vi inte bry oss om högergränsvärdet – brottet i funktionen kommer först efter $x=2$, om vi kommer från höger. 

Vad blir gränsvärdet från vänster? :)

Du menar från höger på väg till x=2 vi har funktionsuttryck $k-x^{2 }?$För att det står för x>2 gäller k-x^2 . 

Smutstvätt skrev:

Att försöka rita är alltid bra! :)

För att funktionen ska vara kontinuerlig får det inte finnas något "glapp" i funktionen. På matematiska innebär det att det måste gälla att $\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }f\left(x\right)=f\left(2\right)$. 

Värdet av $f(2)=2^2=4$, eftersom $f(x)$ definieras som $x^2$ då $x=2$. Från höger påväg till $x=2$ har vi en och samma funktionsuttryck, $f(x)=x^2$, som är ett polynom. Polynomfunktioner är alltid kontinuerliga, om inget annat anges. Därför behöver vi inte bry oss om högergränsvärdet – brottet i funktionen kommer först efter $x=2$, om vi kommer från höger. 

Vad blir gränsvärdet från vänster? :)

Jag hänger tyvärr inte med din resonemang:/

Förstod inte var i grafen du menar. För [-2,2] gäller x^2

men om du menar vänstra gränsen efter x=-2 då blir det $li{m}_{x\to -2^{- }}f\left(x\right) = lim{ }_{x\to -2^{-}} k-x^{2 } = 4$

Denna tråd försvann i min inkorg, och jag missade att svara på den. Nedan finns en fullständig lösning för framtida personer med liknande frågor.

Detta är en längre version av facits lösning, som förhoppningsvis är lite enklare att följa. En skiss av grafen, för olika värden på k, ser ut såhär: 

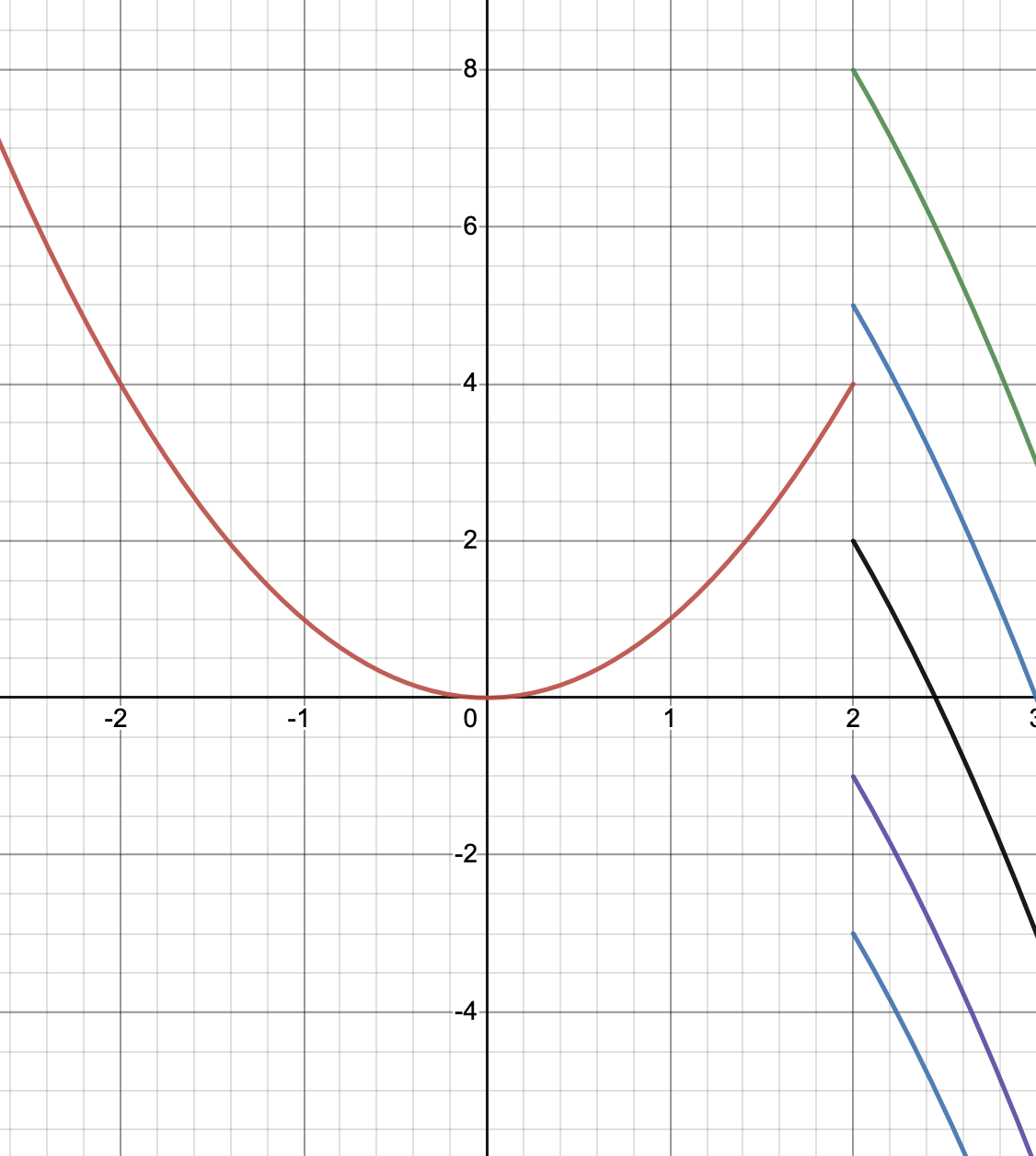
En funktion är kontinuerlig om den inte har några "hopp", dvs. ingenstans där funktionen inte sitter ihop (obs! En funktion kan vara kontinuerlig, förutom ett visst ställe!). Ett exempel på "hopp" är detta: 

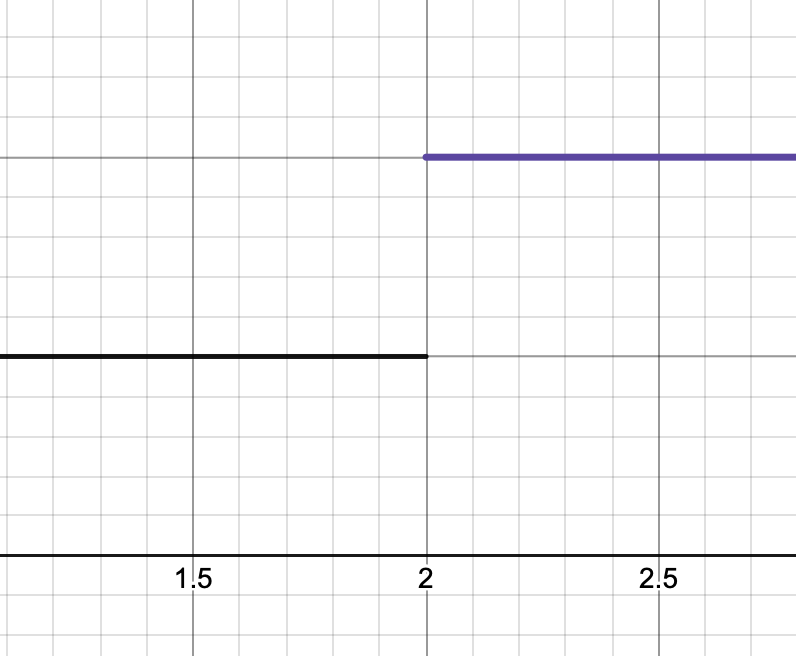
Matematiskt kan detta skrivas som:

Funktionen f är kontinuerlig i den punkt där $x=a$ om $f\left(a\right)=\underset{x\to a}{\lim } f\left(x\right)$. 

Om detta är uppfyllt för alla a i funktionen f:s definitionsmängd, är f kontinuerlig. 

Polynomfunktioner är, om det inte anges några undantag, kontinuerliga. Funktionen som anges i uppgiften är alltså kontinuerlig, förutom i punkten $x=2$, oavsett värde på k. Vi vill nu hitta det värde på k som gör att hela funktionen är kontinuerlig, inklusive $x=2$. 

Enligt vår definition ovan innebär detta att:

$f\left(2\right)=\underset{x\to 2}{\lim } f\left(x\right)$

Det underlättar att titta på gränsvärdet i högerledet som ett höger- och ett vänstergränsvärde, dvs. 

$f\left(2\right)=\underset{x\to 2^{+}}{\lim } f\left(x\right)=\underset{x\to 2^{-}}{\lim } f\left(x\right)$

Värdet i punkten $x=2$ är, enligt definitionen av f(x), $f(2)=2^2=4$. Vänstergränsvärdet ges av $\underset{x\to 2^{-}}{\lim } f\left(2\right)=\underset{x\to 2^{-}}{\lim } \left(x^2\right)$, som vi kan beräkna direkt med $f(2)$, eftersom funktionen är definierad då $x=2$. 

Då kvarstår högergränsvärdet: 

$\underset{x\to 2^{+}}{\lim } f\left(x\right)=\underset{x\to 2^{+}}{\lim } \left(k-x^2\right)=k-\underset{x\to 2^{+}}{\lim } \left(x^2\right)=k-2^2=k-4$

(k påverkas inte av värdet av x, och därför kan vi flytta ut det från gränsvärdet).

Detta gränsvärde ska vara lika med värdet i punkten, vilket ger oss ekvationen:

$$\begin{gathered} \underset{f\left(2\right)}{\underbrace{4}}=\underset{\underset{x\to 2^{-}}{\lim } \left(k-x^2\right)}{\underbrace{k-4}} \\ k=8 \end{gathered}$$

Svar: $k=8$.

Om vi nu ritar upp funktionen $f(x)$ med detta värde på k, kan vi se att funktionen nu är sammanhängande även då 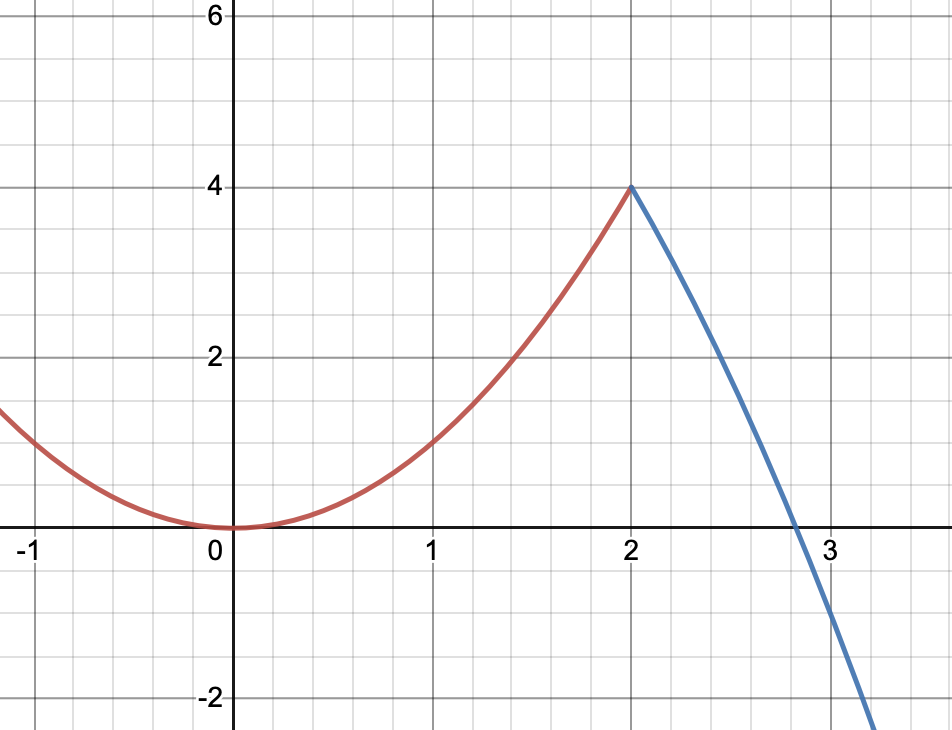$x=2$:

Så vårt svar stämmer. :)