Konservburksproblem
Uppgiften vi ska lösa lyder så här: Du har av en förpackningsindustri fått i uppdrag att utforma en ny serie konservburkar. Ditt uppdrag är att hitta de proportioner på burkarna som gör att materialåtgången blir så liten som möjligt.
· Anta att man kan skära ut alla delar till en cylinderformad konservburk utan att man gör några materialförluster. Bestäm förhållandet mellan höjden h och radien r till en cylinderformad konservburk som gör att materialåtgången blir så liten som möjligt.
· Nu är det inte möjligt att skära ut topp och botten till konservburken utan att göra materialförluster. Anta därför att topp och botten skärs ut ur en kvadratisk skiva med sidlängden 2r. Bestäm förhållandet mellan höjden h och radien r som med detta antagande gör materialåtgången så liten som möjligt.
· Ännu mindre materialspill får man om man skär ut topp och botten ur en skiva med formen av en regelbunden sexhörning. Bestäm förhållandet mellan höjden h och radien r som med detta antagande gör materialåtgången så liten som möjligt.
· Bege dig till en livsmedelsaffär och kontrollmät förhållandet mellan höjd och radie för olika konservburkar. Vilka avvikelser finner du från dina beräkningar? Ge en rimlig förklaring till eventuella avvikelser mellan resultaten av dina beräkningar och de burkar du hittade i affären
Jag har (typ) löst frågorna med hjälp av andra, men förstår inte varför jag ska ta A'(r) = 0 för att få minsta materialtillgång.
På delen med sexhörningen förstår jag inte hur man tar fram arean. Det jag förstår är att man ska dela upp det som 6 trianglar på toppen och botten + att man ska ta mantelarean för den långa delen. På tidigare trådar av samma upgift menar dem att man beräknar arean som;
A=6⋅r^2⋅tan(α/2) +6⋅r^2⋅tan(α/2) +2⋅π⋅r⋅h
Men jag fattar inte varför man ska ta tan.
Tack på förhand för hjälpen!
tan behövs ej. Det är en regelbunden hexagon och du får 6 liksidiga trianglar vars höjd är r.
men vad menas med dehär då?;

Tompayoo skrev:men vad menas med dehär då?;
Det är ett omständigt sätt att lösa en enkel geometrisk figur. Det blir 6 liksidiga trianglar med höjden r och det är samma sak som 12 halva liksidiga trianglar med höjden r som då automatiskt har basen r/sqrt(3).
men jag fattar fortfarande inte vad jag ska skriva för att få roten ur 3 i nämnaren
Var börjar det bli oklart för dig?
Hela del 3 med den sexkantiga plåten. Jag blir superförvirrad
Tompayoo skrev:Hela del 3 med den sexkantiga plåten. Jag blir superförvirrad
Blir detta tydligare?
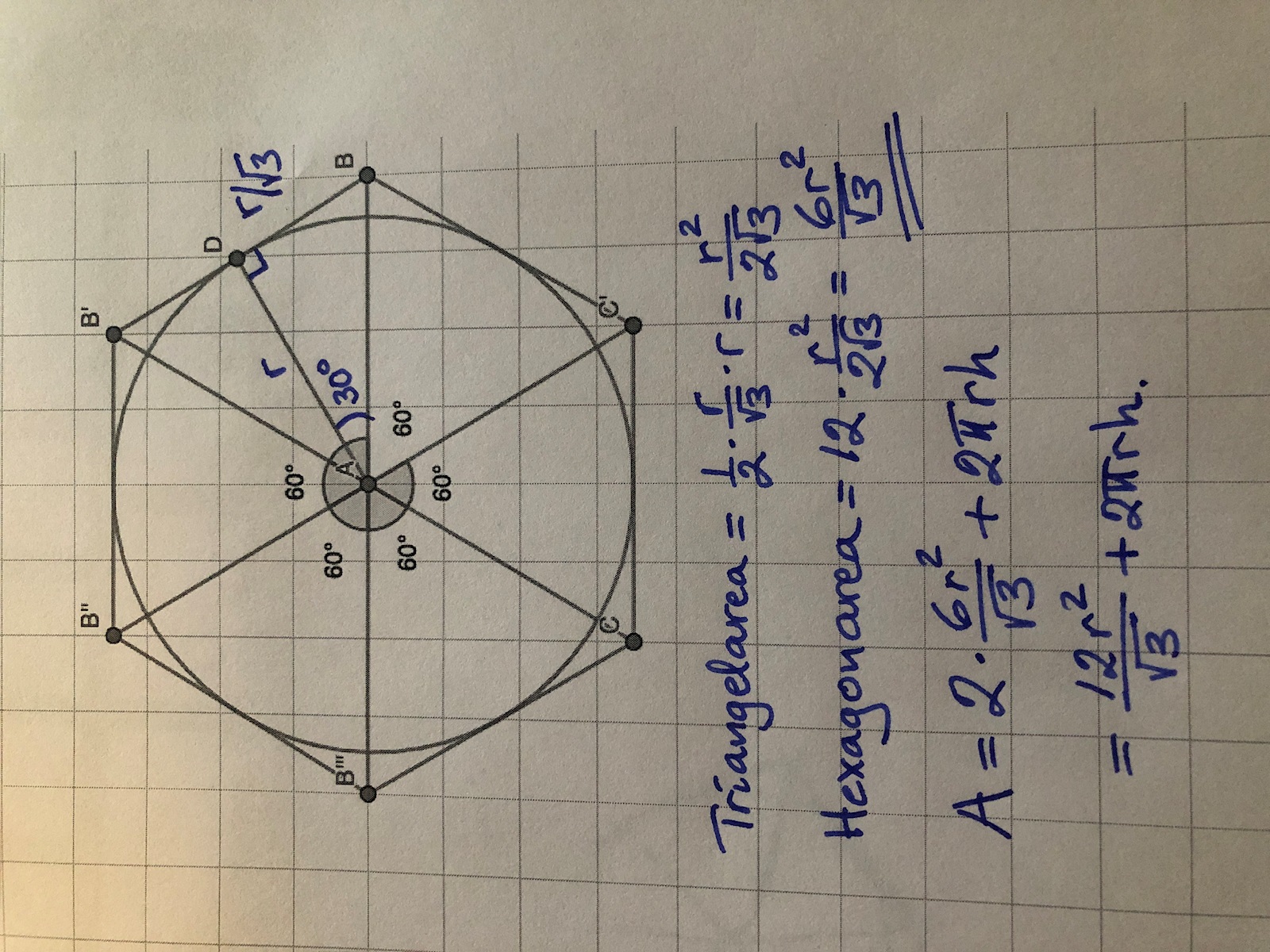
jag förstår inte vart roten ur 3 kommer ifrån, hos r/roten ur 3?
Tompayoo skrev:jag förstår inte vart roten ur 3 kommer ifrån, hos r/roten ur 3?
Det är en 'egenskap' hos 30-60-90-trianglar. Det är en mycket viktig triangel som man bör kunna 'utantill. Den behandlas säkert grundligt i din lärobok.
ber om ursäkt att det är lite suddigt
 Stämmer detta?
Stämmer detta?


