Komplexa tal - belopp av e^2i

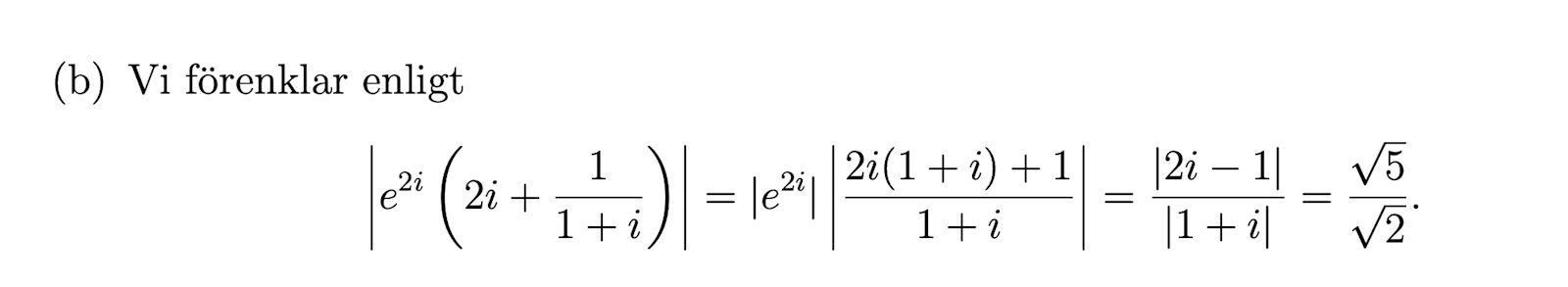
Har du hört talas om Eulers formel?

Ja det har jag, tänker du på e^x(cosy+isiny)? men med insättning av 2=y - hur blir det då?

Nej, jag tänker på att e^iv = cos(v)+i•sin(v).

Det ger att e²ⁱ = cos(2)+i•sin(2).

Beloppet får du sedan med trigonometriska ettan.

men hur blir det då med hänsyn till 2orna? blir liksom e^xi alltid 1 för något reellt tal x?

johannisen skrev:

men hur blir det då med hänsyn till 2orna? blir liksom e^xi alltid 1 för något reellt tal x?

Om du menar ifall |e^xi| alltid är 1 för alla reella x så stämmer det.

I detta fallet:

$|e^{2i}|=|\cos(2)+i\cdot\sin(2)|=$

$=\sqrt{\cos^2(2)+\sin^2(2)}=\sqrt{1}=1$