Lös ekvation med komplexa tal
Hej! Jag har en ekvation som jag ska lösa uppgiften lyder så här:
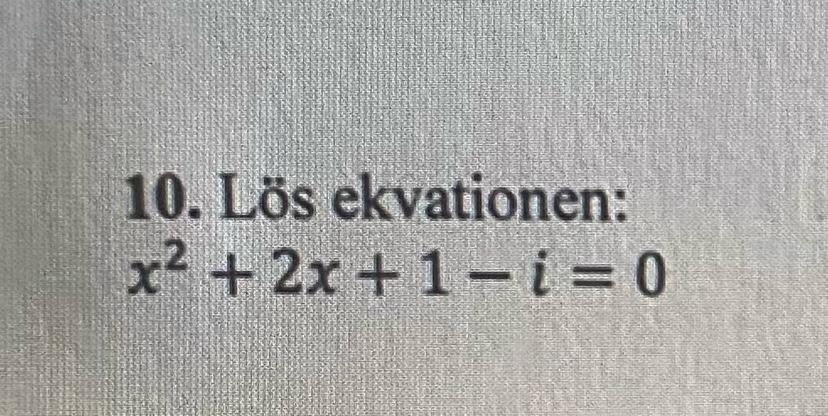
Vet dock inte om jag har löst uppgiften rätt då jag tog med både +1 och -i under rot tecknet (byte tecken också)..... befogar min lösning nedan: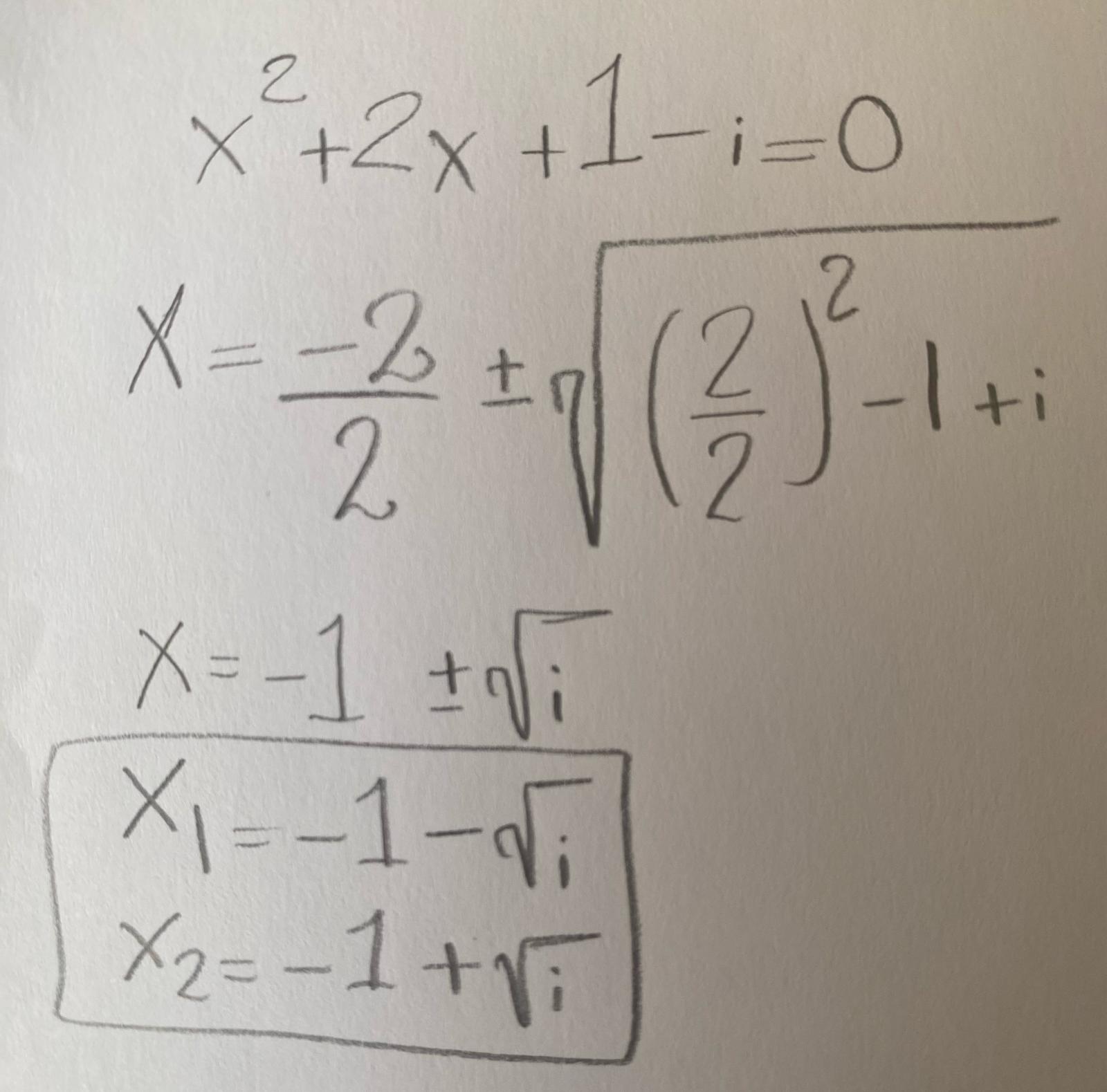 Tack för hjälpen i förhand:)
Tack för hjälpen i förhand:)
Hej.
Din lösning är rätt i princip, men man brukar undvika att svara med komplexa tal under rotenur-tecken.
Om du vill skriva om som ett komplext tal på rektangulär form så kan du göra på följande sätt:
Sätt
Kvadrera båda sidor, vilket ger dig
Utveckla kvadraten och förenkla högerledet. Detta ger dig
Du har nu ett komplext tal i VL och ett komplext tal i HL.
För att dessa två tal ska vara lika måste det gälla att både real- och imaginärdelarna är lila.
Det ger oss för
- Realdelarna att , dvs
- Imaginärdelarna att , dvs
Om du nu kombinerar dessa två ekvationer får du , dvs , dvs
Kommer du vidare därifrån?
Nej! Jag förstod faktiskt inte hur jag ska tänka vidare. Uppskattar om du skrover hela lösningen så det bli lättare och följa efter och förstå :)
Du vet att och att .
Då kan du bestämma de möjliga värdena på både och och sedan konstruera de möjliga kandidaterna till på formen .
Avsluta med att kontrollera att omskrivningen verkligen stämmer, dvs att .
Har jag löst hel uppgiften rätt nu?
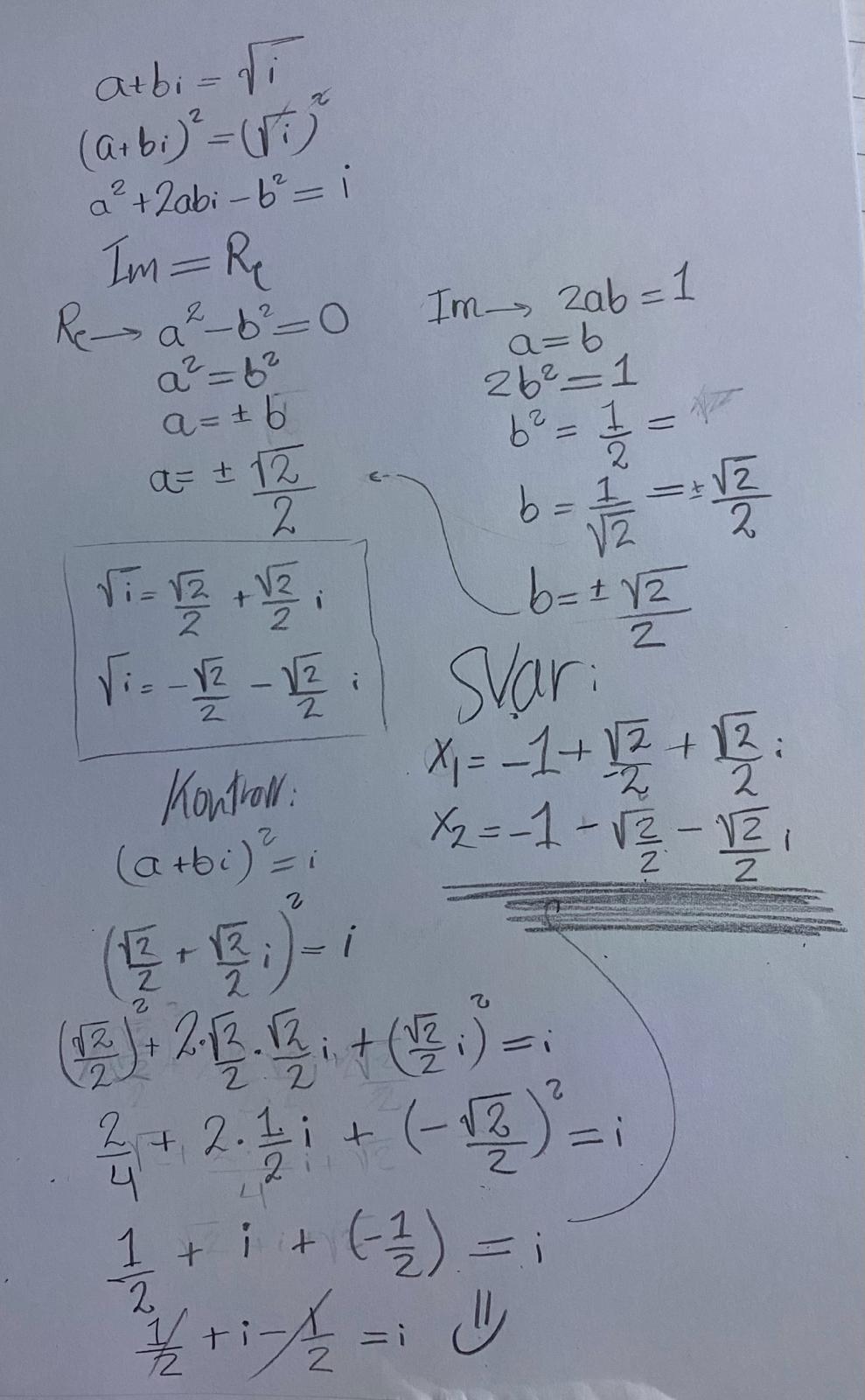
Jag har en del kommentarer, se numrering i bilden.
- Här skriver du Im = Re, vad betyder det?
- Här ska det stå
- Här ska det stå
- Här testar du endast den ena lösningen

Jag har två frågor:
1: Jag får inte i när jag kontrollerar den andra lösningen utan jag får -i, var har jag gjort för fel?
2: Är svaret som jag skrev i rutan rätt?, det vill säga ska jag svara med

Kan någon hjälpa mig vidare tack :)
Här är ett fel i din kontroll.
Bara en av de gulmarkerade faktorerna ska ha ett minustecken framför sig, alternativt att produkten har ett plustecken framför sig.

Förklaring:
Antingen tolkar du uttrycket som och använder andra kvadreringsregeln med och
eller
så tolkar du uttrycket som och använder första kvadreringsregeln med och
=====
Men jag tror att jag krånglade till det i onödan.
Gör istället så att du skriver på polär form (gärna exponentialform, dvs ) och att du sedan drar roten ur detta, dvs att du upphöjer uttrycket till 1/2.
det blir
hur gör jag sen
Skriver om det till formen z = a+bi. Du vet att absolutbeloppet är 1 och att vinkeln är pi/4.
Ja, det stämmer.
Du kan även skriva ut de exakta värdena av de trigonometriska funktionerna.
Ursäkta mig men jag bli lite förvirrad, vad ska jag skriva som svar egentligen? och behöver jag skriva upp allt detta?
Du skall svara på frågan i uppgiften, d v s ta reda på rötterna till ekvationen, och skriva lösningarna på ett "snyggt" eller åtminstone begripligt sätt.
Okej, men har jag inte gjort det i min lösning? ( Dvs att jag har löst uppgiften och gett svaren)?
shadosi skrev:Okej, men har jag inte gjort det i min lösning? ( Dvs att jag har löst uppgiften och gett svaren)?
Vilket är ditt svar? Jag ser en massa kladdiga uträkningar, men inte någon ordentlig lösning.
shadosi skrev:
Jag skrev att det stämmer, men det gör det inte.
Det ska stå
Om du skriver ut detta med hjälp av numeriska värden får du att
Tillsammans med din lösning i svar #1 får du
och



