Beräkna komplext tal med exponent
Hej jag behöver hjälp med denna fråga har försökt lösa den med behöver hjälp med om jag tänker rätt eller inte kommer bifoga både frågan och min lösning här nedan: ( känns som om jag behöver skriva mer i b)
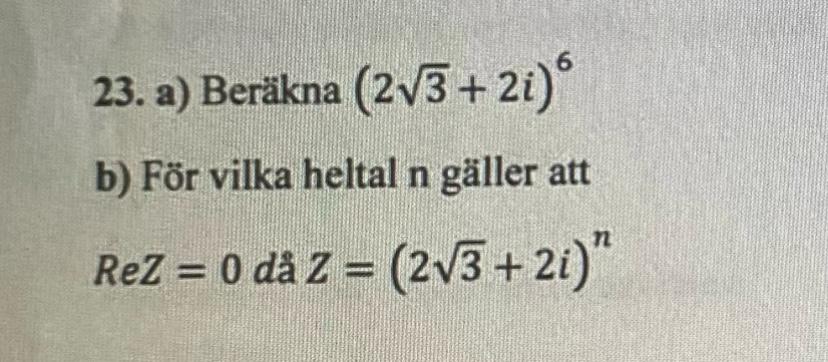

Hej.
Tanken är nog att du ska använda de Moivres formel till denna uppgift.
Dvs börja med att skriva om uttrycket på polär form och bilda sedan ( i b-uppgiften) med hjälp av formeln.
På b-uppgiften kanndu sedan fundera på vilka vinklar som gör att villkoret är uppfyllt.
Då är det till hjälp att använda en illustration med hjälp av det komplexa talplanet.
Hej igen! Jag förstår inte riktigt vad du menar!
Vet du vad polär form är och hur man skriver ett komplext tal på polär form?
Om nej, läs om det här och fråga sedan oss om allt du vill att vi förklarar närmare.
Om ja, läs avsnittet jag länkade till tidigare om de Moivres formel och fråga sedan oss om allt du vill att vi förklarar närmare.
Om du redan är bekant med båda dessa begrepp så ber jag dig att försöka beskriva vad det är du fastnar på?
Hur ska jag fortsätta nu?
Är detta lösningen på a)?

Bra, du tänker och räknar rätt, men skriver lite fel på raden där du bestämmer vinkeln.
Det gäller alltså att det komplexa talet kan skrivas
Använd nu de Moivres formel för att ta fram uttryck för I a-uppgiften och för I b-uppgiften.
Hur ska jag fortsätta nu?
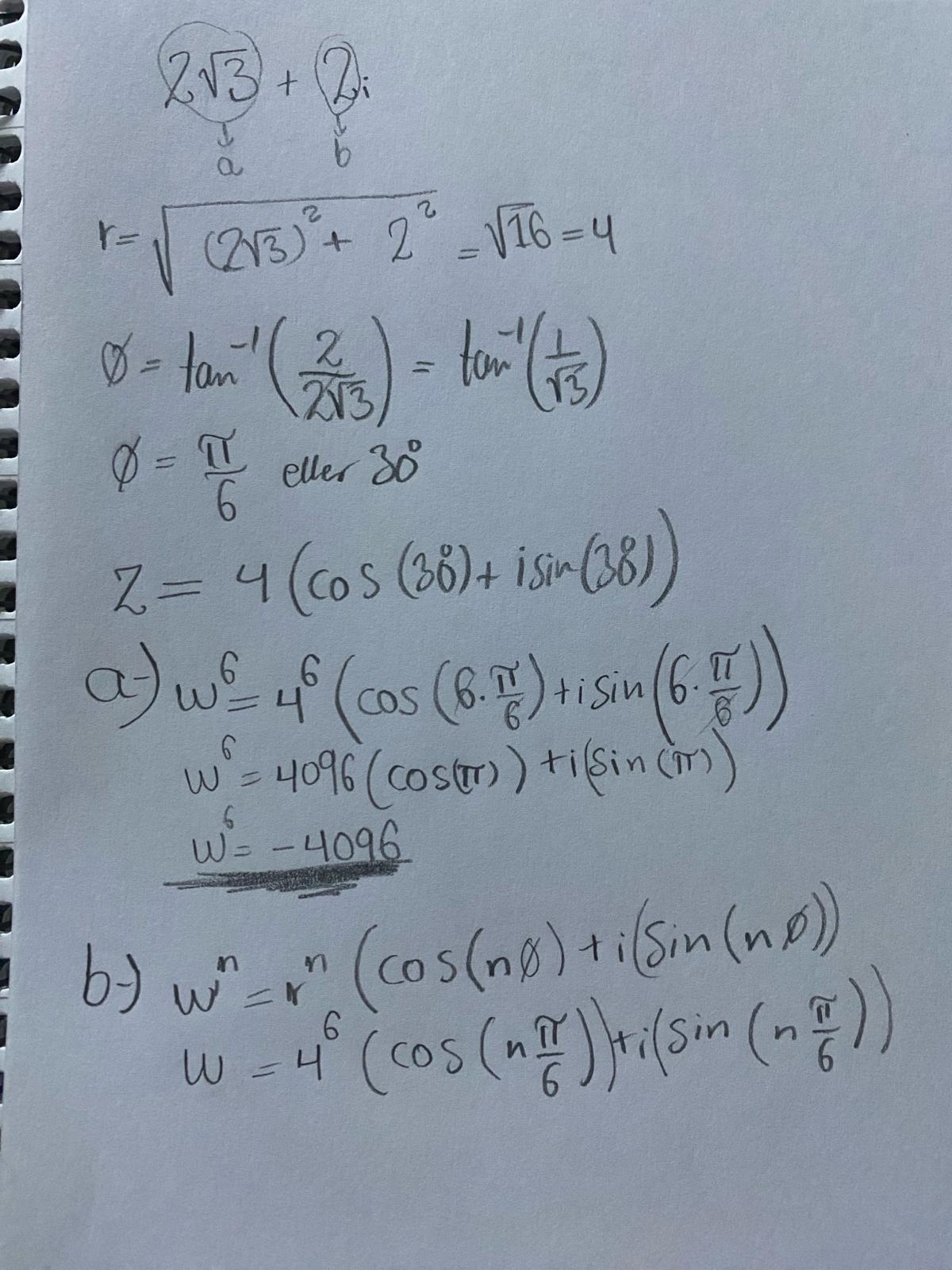
Kan någon hjälpa mig vidare tack :) Uppskattar all hjälp
Titta på:
När blir ReZ=0?
vid !?
Vilket värde har n då?
Finns det någon annan vinkel som ger Re = 0?
Jag känner mig dum:( Förstår inte vad du menar?
För att Re=0 måste cos(n*Pi/6) vara 0.
Alltså kan du lösa ekvationen:
cos(n*Pi/6)=0 , där n måste vara heltal.
Är det rätt så?
Ditt svar på a-uppgiften är rätt, men du har skrivit z = 4(cos(30°)+i*sin(30°)) istället för w = 4(cos(30°)+i*sin(30°)).
Tips: Räkna med grader eller radianer. Blanda inte.
På b-uppgiften skrev du i svar #7 att w = 46(...) men det ska vara z = 4n(...).
I svar #14 har du en bra början, dvs att
Men denna ekvation har två lösningsmängder, nämligen
och
Använd enhetscirkeln för att övertyga dig om det.
Lös nu ut ur de båda ekvationerna.
Jag har rättat alla kommentarerna nu: Ser svaret rätt ut dvs att n=-3 eller 3?
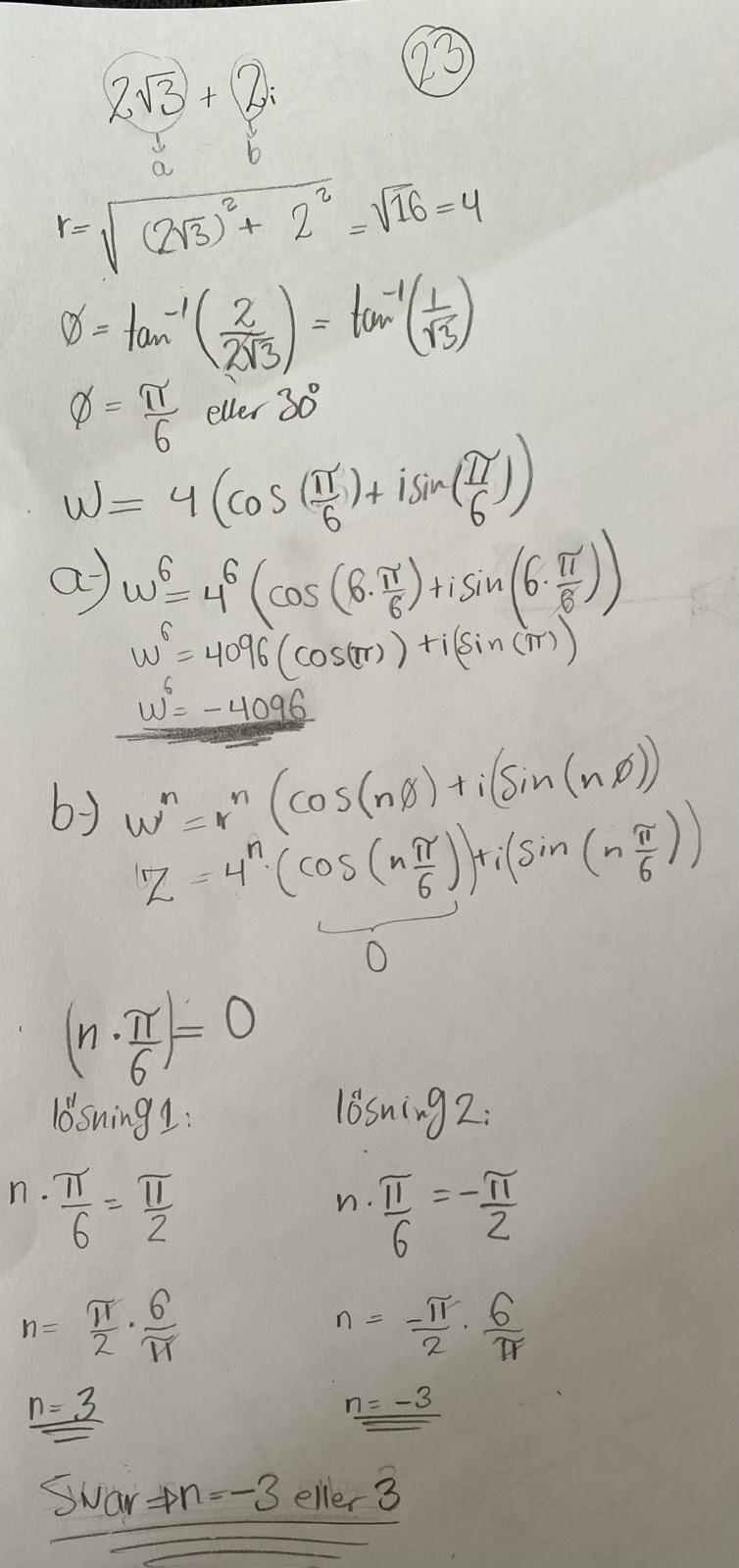
Kan någon hjälpa mig vidare tack :)
Hej, jag ser två fel i din lösning:
- Här ska det stå
- Här missar du att skriva ut periodiciteten I högerleden. De ska vara respektive





