Komplexa tal
Hej! Får verkligen inte ihop det i vad som är sant & falskt. I A, E har jag ingen anning hur man ska tänka. Men i c & d tror jag kommit fram till att d borde vara falskt & c sant. Eftersom alla helttal kan utfryckas som en kvot (dvs Q) & vid additonen försvinner im(z). 
Håller med om att C är sant och D är falskt.
På fråga A är det viktigt att komma ihåg att komplexa talen inkluderar reella talen. T.ex är 45 ett komplext tal.
Med det sagt är det okej att kvoten inte är imaginär, dvs att kvoten är reell, även då både täljaren och nämnaren är imaginära. Vidare ska vi notera att komplexa talen är en sluten grupp under multiplikation (därmed även division då nämnaren kan uttryckas som en multiplikativ invers, dvs 1/någonting). Därmed kommer kvoten alltid ge ett komplext tal (förutsatt att nämnaren är nollskild).
B ser det ut som att du har tänkt rätt på? n=1 (mod 4) gör att n=1,5,9,13,...=4k+1 för alla heltal k.
i^(4k)=1 där k är heltal, därmed gäller att i^(4k+1)=i^1=i.
På E är det bara att bryta ut VL så ser du vad det blir.
Oki tack så mycket! Då har jag iaf kommit fram till c & b korrekt och att d. Är fel. Men förstår inte hur menar du på e & a?
försökt mig på e men det blir helt anurrigt känns som jag krånklar till det!:)

A: Tänk på reella talen. Om du multiplicerar ett reellt tal med ett annat kommer resultatet alltid vara ett reellt tal. Därmed är reella talen sluten under multiplikation (Dock ingår inte 0 eftersom att 0 inte har någon multiplikativ invers, men det behöver vi inte fokusera på här). Samma sak gäller för de komplexa talen, de är slutet under multiplikation. Nästa steg är att inse att multiplikation och division är samma sak, men i division multiplicerar vi med inversen till nämnaren. Sålänge inte nämnare är 0 kommer dess invers existerar och därmed är även de komplexa talen slutet under division. Kvoten mellan två nollskilda komplexa tal blir således ett komplext tal.
E: Bryt ut VL som du skulle ha gjort för en vanlig andragradsekvation.
z2 behöver du inte ändra eftersom att du har en sådan term i HL. Fokusera istället på de andra termer som skiljer sig.
-z*z0 = -(Re(z)+Im(z))*(Re(z0)-Im(z0))=...
E) fråga är (z0)^2 & |z0^2| då samma sak också dvs de tar också ut varandra? precis som z^2?
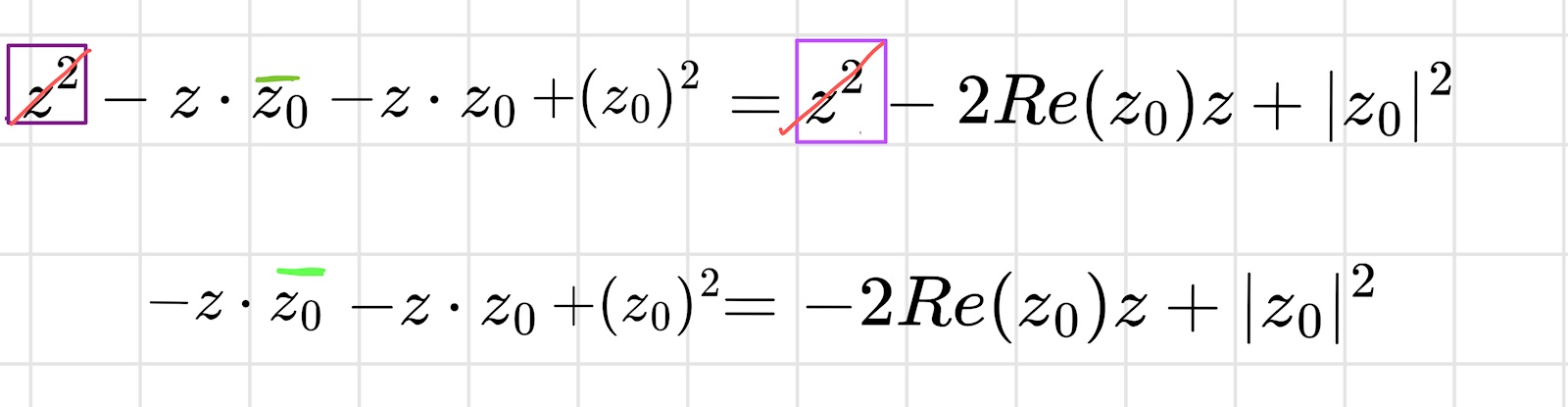
Detta har jag fått nu men vet inte hur jag kommer vidare
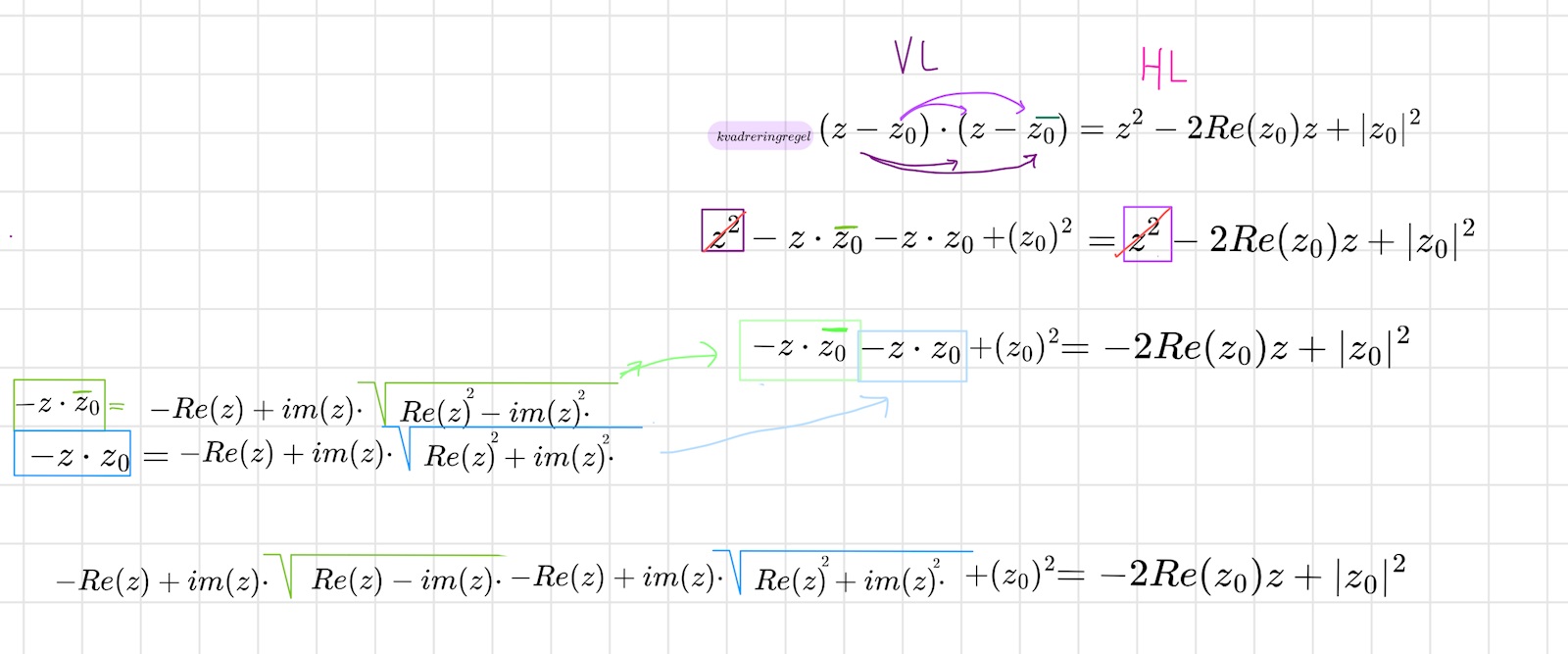
la även in -z•z0- & -z•z0.
bryter ut (-re(z) + im(z) i VL
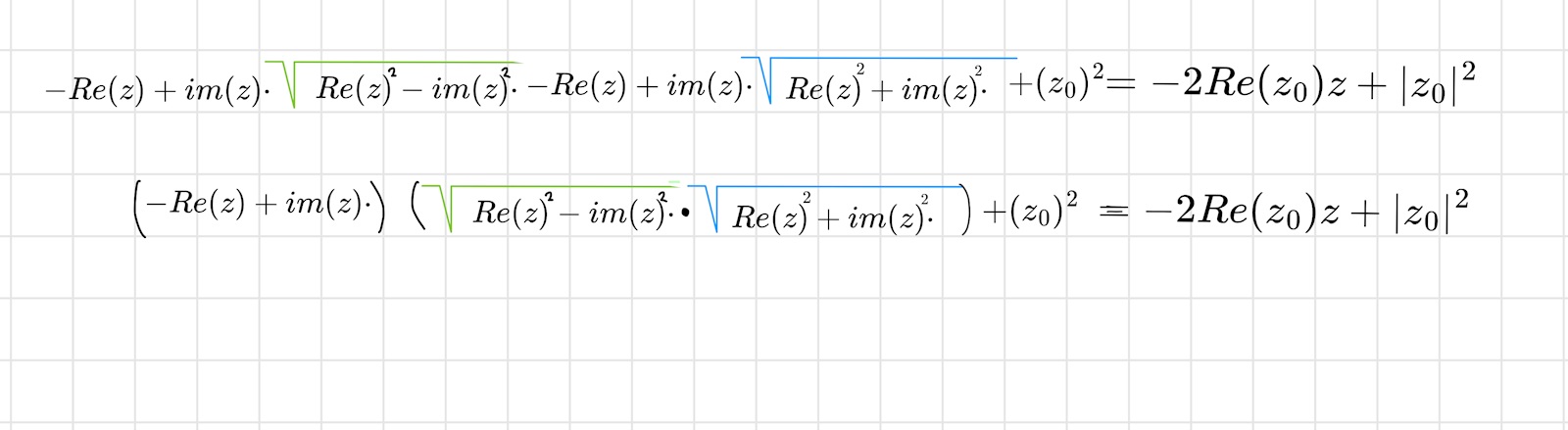
Du har -(Re(z)+Im(z))*(Re(z0)-Im(z0)) - (Re(z)+Im(z))*(Re(z0)+Im(z0))
= -Re(z)Re(z0)+Re(z)Im(z0)-Im(z)Re(z0)+Im(z)Im(z0) - Re(z)Re(z0)-Re(Z)Im(z0)-Im(z)Re(z0)-Im(z)Im(z0)
= -2Re(z)Re(z0) - 2Im(z)Re(z0)
=-2Re(z0)z
men roten ur?
hänger inte riktigt med:)

Tror jag iaf lyckades komma fram till A nu oxå:) Genom att ta divitiobs exempel & förlänga med konjugatet:)
Ja, det stämmer.
(Du skrev lite fel på ett ställe, men det syns att du tänkte och räknade rätt.)



