Komplex serie - bestäm konstanter
Uppgift:
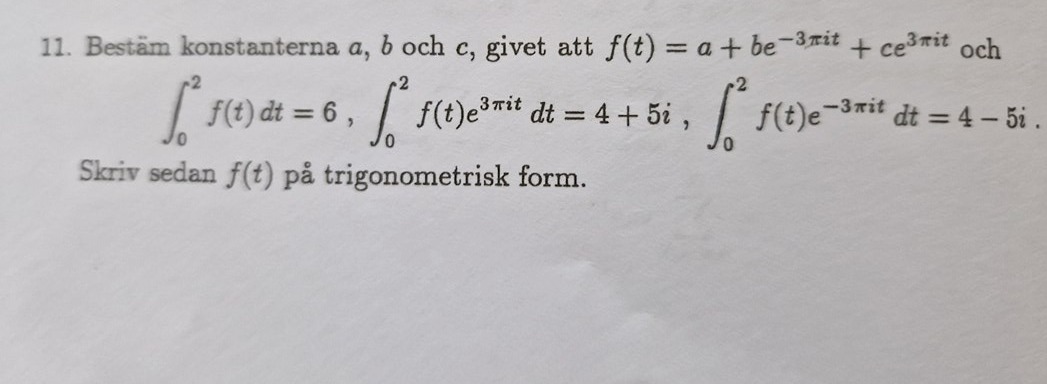
Har löst vad blir, men sitter fast på resten:

Du tittar på fel term; denna integral blir noll. Titta på termen med b istället.
.
PATENTERAMERA skrev:Du tittar på fel term; denna integral blir noll. Titta på termen med b istället.
.
Ok, men varför ?
Ok.
PATENTERAMERA skrev:.
Juste!
Jag inser dock nu att jag inte riktigt förstod teorin bakom när man jobbar med
så blir integranden endast . Varför försvinner resten av termerna i ?
Edit: För det jag kommer fram till är:
Åter igen . Så integralerna över de två sista termerna blir noll. Endast den med a bidrar. De sista termerna är periodiska med medelvärde noll över en period. Du integrerar över ett helt antal perioder, så du får noll.
PATENTERAMERA skrev:Åter igen .
Ja, självklart, det är jag med på nu!
De sista termerna är periodiska med medelvärde noll över en period. Du integrerar över ett helt antal perioder, så du får noll.
Hmm, förstår inte riktigt resonemanget
Ta sinx tex. Den har perioden 2pi. Medelvärdet över en period är .
Så om du integrerar över ett helt antal perioder så får du också noll.
.



