Kommer inte cirkelbanan brytas?
Hur kan stenen fortsätta röra sig i en cirkulär bana om det aldrig tillförs någon ny energi? Ett krav för att rörelsen ska vara cirkulär är väl att farten är konstant?
Så länge snöret är spänt så är ju radien konstant = snörlängden.
Farten är konstant men det är ju fortfarande en accelererande rörelse eftersom hastighetens riktning hela tiden förändras.
Farten kan väl inte vara konstant? Om man slutar snurra stenen kommer väl hastigheten vara lägre längst upp och högre längst ned i rörelsen?
Var har du läst att det är ett krav att farten ska vara konstant?
För att man ska kunna använda
, menar jag.
Det spelar väl ingen roll? Du tar ju reda på kraften i ett ögonblick, och då använder du hastigheten i det ögonblicket.
naytte skrev:Farten kan väl inte vara konstant? Om man slutar snurra stenen kommer väl hastigheten vara lägre längst upp och högre längst ned i rörelsen?
Ja, precis.
Accelerationen är här inte mot cirkelns mitt, vilket är fallet när farten (och radien) är konstant.
Vilken riktning får accelerationen här då?
Accelerationen är i riktningen av den resulterande kraften, vilken är summan av snörkraften riktad mot cirkelns centrum och tyngdkraften riktad nedåt.
Storleken på snörkraften är här inte konstant i rörelsen.
Okej, tack! Ska ge uppgiften ett försök. Återkommer om jag fastnar.
Men bara så att jag förstår, kan man använda formeln jag hänvisade till ovan även i ett särskilt ögonblick i en rörelse? Jag trodde Fc var den kraftsumma som är nödvändig för att hålla föremålet i en cirkelbana. Här varierar såväl spännkraften som hastigheten. Så vad betyder Fc ens i en sådan här situation?
I a)-uppgiften t.ex. ska man använda uttrycket för centripetalkraft. Men jag förstår inte vad en centripetalkraft är i det här sammanhanget. Som sagt förstod jag det som kraften som skulle krävas för att bibehålla en cirkelbana med konstant fart.
Längst upp och längst ner är snörkraft och tyngdkraft parallella. Accelerationen är då riktad mot cirkelns mitt. Du kan i dessa punkter använda att a = v2/R.
Men kommer inte det uttrycket också från uttrycket för centripetalkraften? Det jag inte kan greppa är vad centripetalkraft ens innebär i en situation där farten ständigt förändras. Eller kan man tänka att den rör sig i en cirkelbana "endast i de punkterna"?
Från Wikipedia:
"För det fall då ett objekt rör sig med varierande hastighet i en cirkulär bana kan den nettokraft som påverkar objektet delas upp i två mot varandra vinkelräta komponenter som dels ändrar objektets riktning (centripetalkraften) och en tangentiell som ändrar objektets hastighet."
Är Fc lika stor i varje punkt av cirkelbanan i vårt fall?
Nej, inte lika stor. T.ex är v uppe och nere i rörelsen olika.
Jag har sett många missförstånd om centripetalkraft under åren. Centripetalkraft betyder bara att kraften är riktad mot rörelsens centrum. Sedan kan denna kraft uppstå på olika sätt, t.ex gravitation, snörkraft, friktion, etc.
Sedan är det så att om något rör sig i en cirkelbana med konstant fart, så är accelerationen (och då den resulterande kraften) riktad mot rörelsens centrum.
Jag börjar känna mig riktigt dum nu.
När vi härledde uttrycken och byggde hela härledningen på att farten v var konstant. Men det måste alltså inte vara så?
Härledning vi gick igenom är samma som finns här:
Formeln ac = v2/r gäller även då farten v inte är konstant. Men då tillkommer även accelerationskomposant at som är tangentiell till banan. För denna gäller at = dv/dt.
Du kan hitta en geometrisk härledning av detta i Feynman Lectures Vol I, 11-6.
För att krångla till det mer så kan jag nämna att t.ex. jordbanan inte är cirkulär utan elliptisk. Centripetalkraften är solgravitationen.
PATENTERAMERA skrev:Formeln ac = v2/r gäller även då farten v inte är konstant. Men då tillkommer även accelerationskomposant at som är tangentiell till banan. För denna gäller at = dv/dt.
Du kan hitta en geometrisk härledning av detta i Feynman Lectures Vol I, 11-6.
Tack så mycket för länken! Om det inte är en alltför stor tjänst att be om, skulle du kunna rita in nettoaccelerationen och dess komposanter i följande bild?: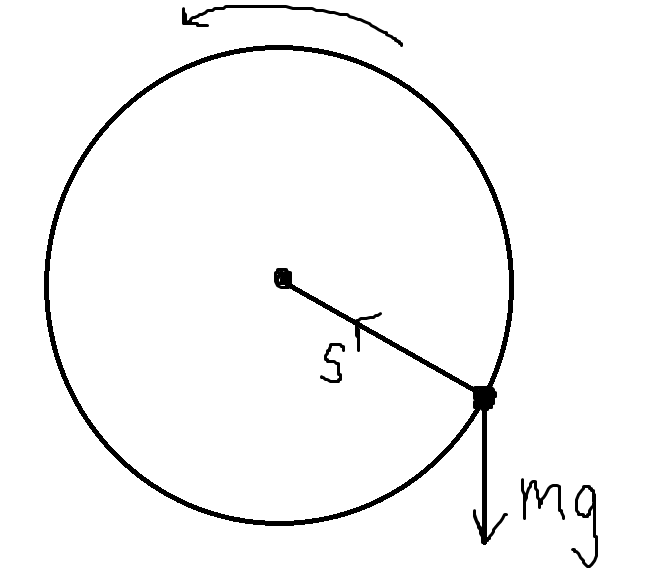
Bilden ska föreställa situationen som uppgiften beskriver. Stenen befinner sig i ett läge lite över sitt understa läge och är på väg upp.
Ja, okej. Så den ena accelerationskomposanten minskar hastighetens storlek medan den ändra ändrar hastighetens riktning? Nu tror jag att jag förstår utdraget som @mrpotatohead hänvisade till, också. Vi får F=ma dels tangentiellt mot rörelsen och dels centripetalt.
Och så länge snöret är spänt hela banan kommer det bli en cirkelbana, eftersom radien då blir samma?
Jepp.
Men detta förutsätter då att snöret alltid är spänt. Så om hastigheten minskar för mycket t.ex, kan cirkelbanan brytas då? Eftersom snöret blir "slappt"? Och om hastigheten blir för stor, kan snöret gå av då?
Ja, på båda.
Tack så hemskt mycket för all hjälp! Nu tror jag att jag äntligen förstår!
Hej, igen! Vill bara bekräfta att jag har gjort rätt då mitt och facits svar skiljer sig åt med några decimaler:
Ser det rätt ut?
I facit har de gjort så här:
Är det bara att de har avrundat som gör att de får 1.43 N istället för 1.36 N?
Lite svårt att säga när du inte visar några siffror. Jag fick i alla fall samma svar som facit.
Oj, nu fick jag samma också. Jag hade avrundat 21.072 till 21 N. Det var där decimalerna försvann.
